(本小题满分9分)以下是用二分法求方程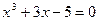 的一个近似解(精确度为0.1)的不完整的过程,请补充完整。
的一个近似解(精确度为0.1)的不完整的过程,请补充完整。
| 区间 |
中点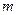 |
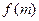 符号 符号 |
区间长度 |
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
解:设函数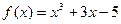 ,其图象在
,其图象在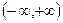 上是连续不断的,且
上是连续不断的,且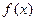 在
在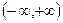 上是单调递______(增或减)。先求
上是单调递______(增或减)。先求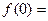 _______,
_______,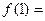 ______,
______,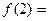 ____________。
____________。
所以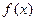 在区间____________内存在零点
在区间____________内存在零点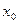 ,再填上表:
,再填上表:
下结论:_______________________________。
(可参考条件: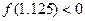 ,
,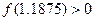 ;符号填+、-)
;符号填+、-)
从某校高一年级随机抽取 名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
| 组号 |
分组 |
频数 |
频率 |
| 1 |
[5,6) |
2 |
0.04 |
| 2 |
[6,7) |
0.20 |
|
| 3 |
[7,8) |
a |
|
| 4 |
[8,9) |
b |
|
| 5 |
[9,10) |
0.16 |

(I)求 的值;
的值;
(Ⅱ)若 ,补全表中数据,并绘制频率分布直方图;
,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替。若上述数据的平均值为7.84,求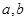 的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率。
的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率。
(本小题满分10分)选修4—5:不等式选讲
设 .
.
(1)求 的解集;
的解集;
(2)若不等式 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程
的参数方程 (
( 为参数).以
为参数).以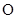 为极点,
为极点,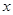 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线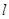 的极坐标方程是
的极坐标方程是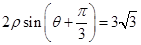 ,射线
,射线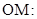
 与圆
与圆 的交点为
的交点为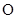 、
、 ,与直线
,与直线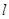 的交点为
的交点为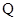 ,求线段
,求线段 的长.
的长.
(本小题满分10分)选修4—1:几何证明选讲
如图所示,已知圆 外有一点
外有一点 ,作圆
,作圆 的切线
的切线 ,
,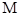 为切点,过
为切点,过 的中点
的中点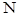 ,作割线
,作割线 ,交圆于
,交圆于 、
、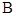 两点,连接
两点,连接 并延长,交圆
并延长,交圆 于点
于点 ,连接
,连接 交圆
交圆 于点
于点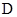 ,若
,若 .
.
(1)求证: ∽
∽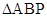 ;
;
(2)求证:四边形 是平行四边形.
是平行四边形.
(本小题满分12分)函数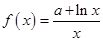 ,若曲线
,若曲线 在点
在点 处的切线与直线
处的切线与直线 垂直(其中
垂直(其中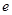 为自然对数的底数).
为自然对数的底数).
(1)若 在
在 上存在极值,求实数
上存在极值,求实数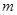 的取值范围;
的取值范围;
(2)求证:当 时,
时, .
.