(本小题满分8分)已知函数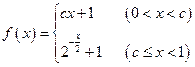 ,满足
,满足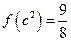
(1)求常数 的值;
的值;
(2)解不等式 .
.
已知函数
(1)求函数 在点(0,f(0))处的切线方程;
在点(0,f(0))处的切线方程;
(2)求函数 单调递增区间;
单调递增区间;
(3)若
 ∈[1,1],使得
∈[1,1],使得 (e是自然对数的底数),求实数
(e是自然对数的底数),求实数 的取值范围.
的取值范围.
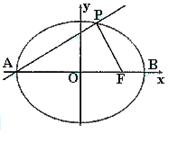
如图,已知椭圆C的中心在原点,焦点在x轴上,离心率为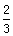 ,且过点
,且过点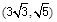 ,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方,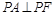 .
.
(1)求椭圆C的方程;
(2)求点P的坐标;
(3)设M是直角三角PAF的外接圆圆心,求椭圆C上的点到点M的距离 的最小值.
的最小值.
数列{an}(n∈N﹡)中,a1=0,当3an<n2时,an+1=n2,当3an>n2时,an+1=3an.求a2,a3,a4,a5,猜测数列的通项an并证明你的结论.
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
 |
5 |
0.050 |
| 第2组 |
 |
① |
0.350 |
| 第3组 |
 |
30 |
② |
| 第4组 |
 |
20 |
0.200 |
| 第5组 |
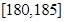 |
10 |
0.100 |
| 合计 |
100 |
1.00 |
(1)请先求出频率分布表中①、②位置相应的数据,再在答题卷上完成下列频率分布直方图;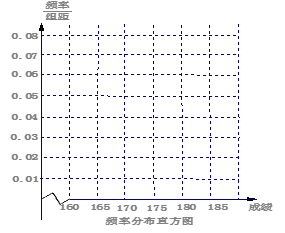
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求:第4组至少有一名学生被考官A面试的概率?
直三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:直线AB1⊥平面A1BD.
(2)求二面角A-A1D-B正弦值的大小.