（本小题10分）
如图，在多面体ABCDEF中，四边形ABCD是正方形，AB=2EF=2，EF∥AB，EF⊥FB,∠BFC=90°，BF=FC.
（1）求证：平面ABFE⊥平面DCFE；
（2）求四面体B—DEF的体积.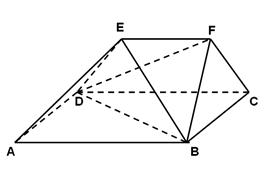
已知函数
为奇函数，且
，其中
（1）求
的值;
（2）若
，求
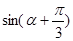的值．
某同学用五点法画函数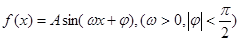
在某一个周期内的图像时，列表并填入了部分数据，如下表：
 |
0 |
 |
 |
 |
 |
 |
 |
 |
|||
 |
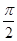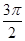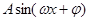0 |
5 |
-5 |
0 |
（1）请将上表数据补充完整，并直接写出函数
的解析式;
（2）若函数的图像向左平移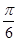
个单位后对应的函数为
，求的图像离原点最近的对称中心
（本小题满分12分）已知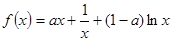
，
（1）当
=2时，求曲线
在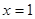
处的切线方程；
（2）若
0，讨论函数
的单调性．
（本小题满分12分）已知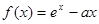
（
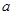为常数）的图象与
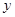轴交于点A，曲线
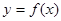在点A处的切线斜率为-1，
（1）求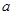的值及函数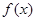
的极值；
（2）证明：当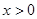
时，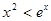
．
（本小题满分12分）已知函数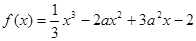
，
（1）若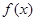
的单调减区间为（-3，-1），求
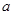的值；
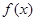（2）若在（0，2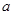）上有两个零点，求
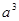的取值范围．