已知f(x)=-3x2+a(6-a)x+b.
解关于a的不等式f(1)>0;
当不等式f(x)>0的解集为(-1,3)时,求实数a,b的值。
已知数列 的各项均为正数,观察程序框图,若
的各项均为正数,观察程序框图,若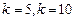 时,分别有
时,分别有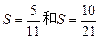 .
.
(1)试求数列 的通项;
的通项;
(2)令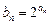 ,求
,求 的值.
的值.
如图,已知向量 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若
 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算 ,显然
,显然 的结果仍为一向量,记作
的结果仍为一向量,记作 .
.
1、求证:向量 为平面
为平面 的法向量;
的法向量;
2、求证:以 为边的平行四边形
为边的平行四边形 的面积等于
的面积等于 ;
;
将四边形 按向量
按向量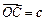 平移,得到一个平行六面体
平移,得到一个平行六面体 ,试判断平行六面体的体积
,试判断平行六面体的体积 与
与 的大小.
的大小.
如图,在三棱锥 中,
中,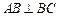 ,
, ,点
,点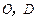 分别是
分别是 的中点,
的中点, 底面
底面 .
.
(1)求证: 平面
平面 ;
;
(2)当 时,求直线
时,求直线 与平面
与平面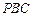 所成角的余弦值;
所成角的余弦值;
(3)当 为何值时,
为何值时, 在平面
在平面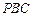 内的射影恰好为
内的射影恰好为 的重心?
的重心?
如图,圆柱OO 内有一个三棱柱ABC—A
内有一个三棱柱ABC—A ,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径。
(1)证明:平面 平面
平面 ;
;
(2)设AB=AA
 ,在圆柱OO
,在圆柱OO 内随机选取一点,记该点取自三棱柱ABC—A
内随机选取一点,记该点取自三棱柱ABC—A B
B
 内的概率为P.
内的概率为P.
①当点C在圆周上运动时,求 的最大值;
的最大值;
②记平面 与平面
与平面 所成的角为
所成的角为
 ,当
,当 取最大值时,求
取最大值时,求 的值。
的值。
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高。然而也有部分公众对该活动的实际效果与负面影响提出了疑问。对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 |
保留 |
不支持 |
|
| 20岁以下 |
800 |
450 |
200 |
| 20岁以上(含20岁) |
100 |
150 |
300 |
⑴在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持”态度的人中抽取了45个人,求n的值;
⑵在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中
任意选取2人,求至少1人20岁以下的概率;
⑶在接受调查的人中,有8人给这项活动打出了分数如下:9.4, 8.6, 9.2, 9.6, 8.7
9.3, 9.0, 8.2.把这8人打出的分数看作一个总体,从中任取一个数,求该数与总体平均数之差的绝对值超过0.6的概率。