(本小题满分13分)已知定义域为R的函数 是奇函数.
是奇函数.
(I)求a的值,并指出函数 的单调性(不必说明单调性理由);
的单调性(不必说明单调性理由);
(II)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
下面是计算应纳税所得额的算法过程,其算法如下:
第一步输入工资x(注x<=5000);
第二步如果x<=800,那么y=0;如果800<x<=1300,那么 y=0.05(x-800);否则 y=25+0.1(x-1300)
第三步输出税款y, 结束。
请写出该算法的程序框图和程序。(注意:程序框图与程序必须对应)
(本小题满分14分)已知向量a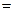
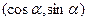 ,b
,b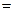
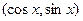 ,
,
c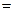

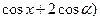 ,其中
,其中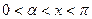 .
.
(1)若 ,求函数
,求函数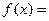 b·c的最小值及相应的
b·c的最小值及相应的 的值;
的值;
(2)若a与b的夹角为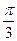 ,且a⊥c,求
,且a⊥c,求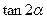 的值.
的值.
(本小题满分12分)已知函数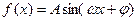
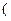
 ,
, ,
,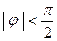
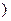
在一个周期内,当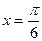 时,
时,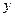 有最大值为
有最大值为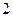 ,当
,当 时,
时,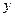 有最小值为
有最小值为  .
.
(1)求函数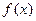 表达式;
表达式;
(2)若 ,求
,求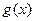 的单调递减区间.
的单调递减区间.
(本小题满分12分)甲乙两人各有 个材质、大小、形状完全相同的小球,甲的
个材质、大小、形状完全相同的小球,甲的
小球上面标有 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有 五个数字.把各自的小球放
五个数字.把各自的小球放
入两个不透明的口袋中,两人同时从各自的口袋中随机摸出 个小球.规定:若甲摸出的小
个小球.规定:若甲摸出的小
球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间 ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.
(本小题满分12分)已知点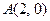 ,
,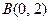 ,点
,点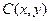 在单位圆上.
在单位圆上.
(1)若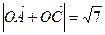 (
(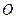 为坐标原点),求
为坐标原点),求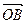 与
与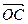 的夹角;
的夹角;
(2)若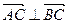 ,求点
,求点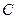 的坐标.
的坐标.