(本小题满分12分)
在 中,内角
中,内角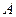 ,
,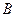 ,
,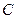 的对边分别为
的对边分别为 ,已知
,已知 ,
,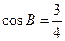
(1)求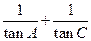 的值;
的值;
(2)设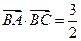 ,求
,求 的值.
的值.



⑴求函数 的解析式;
的解析式;
⑵若对于区间 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数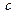 的最小值;
的最小值;
⑶若过点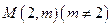 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围
的取值范围

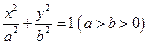




⑴求椭圆 的方程;
的方程;
⑵设 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心,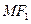 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线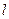 有公共点时,求△
有公共点时,求△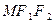 面积的最大值
面积的最大值
如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AB=BC= ,BB1=3,D为A1C1的中点,F在线段AA1上.
,BB1=3,D为A1C1的中点,F在线段AA1上.
(1)AF为何值时,CF⊥平面B1DF?
(2)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值.
已知椭圆 的离心率为
的离心率为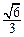 ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且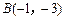 .
.
(1)求椭圆C和直线l的方程;
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若
曲线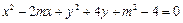 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=6km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y.
(1)设 ,把y表示成
,把y表示成 的函数关系式;
的函数关系式;
(2)变电站建于何处时,它到三个小区的距离之和最小?