为配合新课程的实施，乌鲁木齐市第一中学联合兄弟学校举行了“应用与创新”知识竞赛，共有1500名学生参加了这次竞赛（满分100分，得分全为整数）．为了解本次竞赛成绩情况，从中随机抽取了部分学生的竞赛成绩，进行统计，整理见下表：
| 组别 |
分 组 |
频 数 |
频率 |
| 1 |
49．5～59．5 |
60 |
0．12 |
| 2 |
59．5～69．5 |
120 |
0．24 |
| 3 |
69．5～79．5 |
180 |
0．36 |
| 4 |
79．5～89．5 |
130 |
 |
| 5 |
89．5～99．5 |
 |
0．02 |
| 合 计 |
 |
1．00 |
解答下列问题：
（1）在这个问题中，总体是 ，样本是 ，
样本容量＝ ；
（2）第四小组的频率＝ ；
（3）被抽取的学生成绩的中位数落在第几小组内？
（4）若成绩在90分以上（含90分）的学生获一等奖，请你估计此次竞赛获一等奖的人数．
为拉动经济增长，某市决定新建一批基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目个数分别占总数的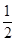
，
，
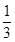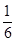，现在3名工人独立地从中任意一个项目参与建设．
(1)求他们选择的项目所属类别互不相同的概率．
(2)记X为3人中选择的项目所属于基础设施工程或产业建设工程的人数，求X的分布列及数学期望．
形状如图所示的三个游戏盘中(图①是正方形，M，N分别是所在边中点，图②是半径分别为2和4的两个同心圆，O为圆心，图③是正六边形，点P为其中心)各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．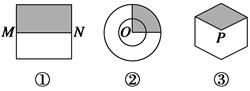
(1)一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？
(2)用随机变量X表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量X的分布列．
学校游园活动有这样一个游戏项目：甲箱子里装有3个白球，2个黑球，乙箱子里装有1个白球，2个黑球，这些球除颜色外完全相同．每次游戏从这两个箱子里各随机摸出2个球，若摸出的白球不少于2个，则获奖(每次游戏结束后将球放回原箱)
(1)求在一次游戏中
①摸出3个白球的概率；②获奖的概率．
(2)求在两次游戏中获奖次数X的分布列及数学期望E(X)．
某居民小区有两个相互独立的安全防范系统(简称系统)A和B，系统A和B在任意时刻发生故障的概率分别为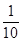
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为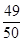
，求p的值；
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ，求ξ的概率分布列及数学期望Eξ.
一投掷飞碟的游戏中，飞碟投入红袋记2分，投入蓝袋记1分，未投入袋记0分．经过多次试验，某人投掷100个飞碟有50个入红袋，25个入蓝袋，其余不能入袋．
(1)求该人在4次投掷中恰有三次投入红袋的概率；
(2)求该人两次投掷后得分ξ的数学期望Eξ.