(本小题12分)
某商店按每件80元的价格,购进时令商品(卖不出去的商品将成为废品)1000件;市场调研推知:当每件售价为100元时,恰好全部售完;在此基础上当售价每提高1元时,销售量就减少5件;为获得最大利润,请你确定合理的售价,并求出此时的利润;
在直三棱柱ABC-A1B1C1中,∠ABC="90°," AB="BC=1."
(1)求异面直线B1C1与AC所成角的大小;
(2)若直线A1C与平面ABC所成角为45°,
求三棱锥A1-ABC的体积.
已知点集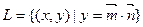 ,其中
,其中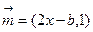 ,
, ,点列
,点列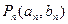 在L中,
在L中,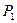 为L与y轴的交点,等差数列
为L与y轴的交点,等差数列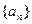 的公差为1,
的公差为1,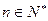 。
。
(1)求数列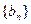 的通项公式;
的通项公式;
(2)若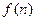 =
= ,令
,令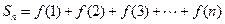 ;试用解析式写出
;试用解析式写出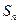 关于
关于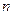 的函数。
的函数。
(3)若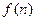 =
= ,给定常数m(
,给定常数m(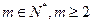 ),是否存在
),是否存在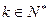 ,使得
,使得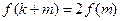 ,若存在,求出
,若存在,求出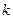 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
在四棱锥 中,
中,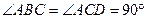 ,
,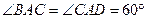 ,
,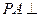 底面
底面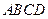 ,
,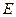 为
为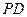 的中点,
的中点,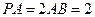 .
.
(Ⅰ)求四棱锥 的体积
的体积 ;
;
(Ⅱ) 求二面角 的大小.
的大小.
某超市为了响应环保要求,鼓励顾客自带购物袋到超市购物,采取了如下措施:对不使用超市塑料购物袋的顾客,超市给予0.96折优惠;对需要超市塑料购物袋的顾客,既要付购买费,也不享受折扣优惠.假设该超市在某个时段内购物的人数为36人,其中有12位顾客自己带了购物袋,现从这36人中随机抽取2人.
(Ⅰ)求这2人都享受折扣优惠或都不享受折扣优惠的概率;
(Ⅱ)设这2人中享受折扣优惠的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
在
上定义运算
(
、
为实常数)。记
,
,
。令
。
(Ⅰ)如果函数
在
处有极值
,试确定
、
的值;
(Ⅱ)求曲线
上斜率为
的切线与该曲线的公共点;
(Ⅲ)记
的最大值为
,若
对任意的
、
恒成立,试示
的最大值。