本题满分12分)
在一条笔直的工艺流水线上有三个工作台,将工艺流水线用如图所示的数轴表示,各工作台的坐标分别为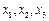 ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在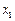 与
与 之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(1)若每个工作台上只有一名工人,试确定供应站的位置;
(2)设三个工作台从左到右的人数依次为2,1,3,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.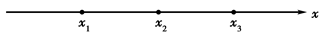
数列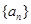 满足
满足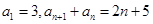 .
.
(1)求 的表达式;
的表达式;
(2)令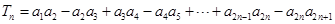 ,求
,求 .
.
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A,B的一点,D为AC的中点. 
(1)求该圆锥的侧面积S;
(2)求证:平面PAC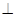 平面POD;
平面POD;
(3)若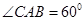 ,在三棱锥A-PBC中,求点A到平面PBC的距离.
,在三棱锥A-PBC中,求点A到平面PBC的距离.
已知正方形ABCD的边长为2,E,F,G,H分别是边AB,BC,CD,DA的中点.
(1)从C,D,E,F,G,H这六个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求概率P
,求概率P .
.
(2)在正方形ABCD内部随机取一点P,求满足 的概率.
的概率.
已知函数
(1)求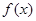 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)已知 是
是 三边长,且
三边长,且 ,
, 的面积
的面积 .求角
.求角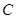 及
及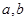 的值.
的值.
已知函数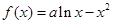 .
.
(1)当 时,求函数
时,求函数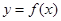 在
在 上的最大值;
上的最大值;
(2)令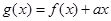 ,若
,若 在区间
在区间 上不单调,求
上不单调,求 的取值范围;
的取值范围;
(3)当 时,函数
时,函数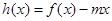 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且 ,又
,又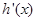 是
是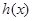 的导函数,若正常数
的导函数,若正常数 满足条件
满足条件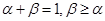 .证明:
.证明: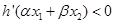 .
.