(本小题满分12分)
如下图,O1(– 2,0),O2(2,0),圆O1与圆O2的半径都是1,

(1) 过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得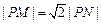 .求动点P的轨迹方程;
.求动点P的轨迹方程;
(2) 若直线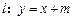 交圆O2于A、B,又点C(3,1),当m取何值时,△ABC的面积最大?
交圆O2于A、B,又点C(3,1),当m取何值时,△ABC的面积最大?
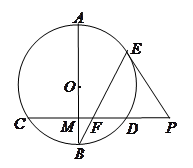
如图,已知⊙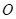 中,直径
中,直径 垂直于弦
垂直于弦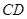 ,垂足为
,垂足为 ,
, 是
是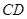 延长线上一点,
延长线上一点, 切⊙
切⊙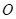 于点
于点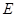 ,连接
,连接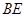 交
交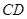 于点
于点 ,证明:
,证明: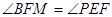
设函数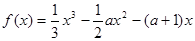
①当a=1时,求函数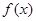 的极值;
的极值;
②若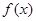 在
在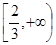 上是递增函数,求实数a的取值范围;
上是递增函数,求实数a的取值范围;
③当0<a<2时, ,求
,求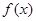 在该区间上的最小值.
在该区间上的最小值.
数列{an}满足an>0,前n项和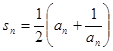 .
.
①求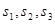 ;
;
②猜想{sn}的通项公式,并用数学归纳法证明.
已知a、b、c、d均为实数,且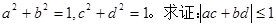 .
.
对于企业来说,生产成本、销售收入和利润之间的关系是个重要的问题.对一家药品生产企业的研究表明,该企业的生产成本y(单位:万元)和生产收入z(单位:万元)都是产量x(单位:t)的函数,分别为: 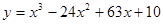 ,Z=18x
,Z=18x
①试写出该企业获得的生产利润w(单位:万元)与产量x之间的函数关系式;
②当产量为多少时,该企业可获得最大利润?最大利润为多少?