(本小题满分15分)已知椭圆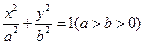 的离心率为
的离心率为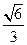 ,过
,过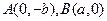 的直线与原点的距离为
的直线与原点的距离为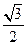
(1)求椭圆的方程;
(2)已知定点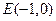 ,直线
,直线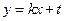 与椭圆交于不同两点C,D,试问:对任意的
与椭圆交于不同两点C,D,试问:对任意的 ,是否都存在实数
,是否都存在实数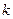 ,使得以线段CD为直径的圆过点E?证明你的结论
,使得以线段CD为直径的圆过点E?证明你的结论
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证: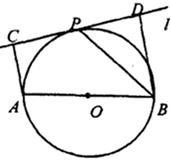
(1)l是⊙O的切线;
(2)PB平分∠ABD.
已知函数f(x)=a|x|+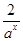 (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)=" f(" x),x∈[ 2,+∞),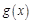 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
已知椭圆C: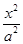 +
+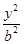 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=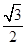 ,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为
,椭圆C的上、下顶点分别为A1,A2,左、右顶点分别为B1,B2,左、右焦点分别为F1,F2.原点到直线A2B2的距离为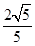 .
.
(1)求椭圆C的方程;
(2)过原点且斜率为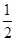 的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交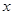 轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
轴于点N,M,若直线OT与过点M,N 的圆G相切,切点为T.证明:线段OT的长为定值,并求出该定值.
如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通.已知AB = 60m,BC = 80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB= α,矩形区域内的铺设水管的总费用为W.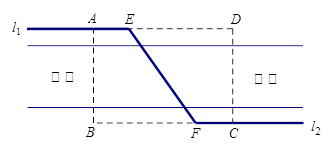
(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α.
已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足bn= ,其前n项和为Sn.
,其前n项和为Sn.
(1)求数列{an}的通项公式;
(2)若S2为S1,Sm (m∈N*)的等比中项,求正整数m的值.
(3)对任意正整数k,将等差数列{an}中落入区间(2k,22k)内项的个数记为ck,求数列{cn}的前n项和Tn