(本小题满分12分)已知函数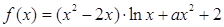 .
.
(Ⅰ)当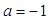 时,求
时,求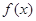 在
在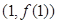 处的切线方程;
处的切线方程;
(Ⅱ)设函数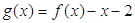 ,
,
①若函数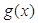 有且仅有一个零点时,求
有且仅有一个零点时,求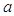 的值;
的值;
②在①的条件下,若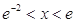 ,
,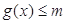 ,求
,求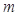 的取值范围。
的取值范围。
从高三学生中抽取50名同学参加数学竞赛,成绩的分组及各组的频数如下:(单位:分)
[40,50),2;[50,60),3;[60,70),10;[70,80),15;
[80,90),12;[90,100],8.
(1)列出样本的频率分布表;
(2)画出频率分布直方图;
(3)估计成绩在[60,90)分的学生比例;
(4)估计成绩在85分以下的学生比例.
为了了解小学生的体能情况,抽取了某小学同年级部分学生进行跳绳测试,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数为5.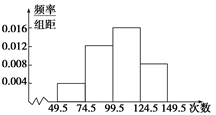
(1)求第四小组的频率;
(2)参加这次测试的学生人数是多少?
(3)在这次测试中,学生跳绳次数的中位数落在第几小组内?
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别
记录抽查数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间产品较稳定.
为了解A,B两种轮胎的性能,某汽车制造厂分别从这两种轮胎中随机抽取了8个进行测试,下面列出了每一个轮胎行驶的最远里程数(单位:1 000 km)
轮胎A 96, 112, 97, 108, 100, 103, 86, 98
轮胎B 108, 101, 94, 105, 96, 93, 97, 106
(1)分别计算A,B两种轮胎行驶的最远里程的平均数,中位数;
(2)分别计算A,B两种轮胎行驶的最远里程的极差、标准差;
(3)根据以上数据你认为哪种型号的轮胎性能更加稳定?
对某电子元件进行寿命追踪调查,情况如下:
| 寿命(h) |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表;
(2)画出频率分布直方图;
(3)估计电子元件寿命在100 h~400 h以内的概率;
(4)估计电子元件寿命在400 h以上的概率.