函数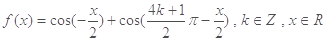 .
.
(1)求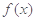 的周期;
的周期;
(2)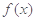 在
在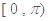 上的减区间;
上的减区间;
(3)若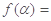
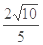 ,
,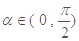 ,求
,求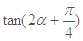 的值.
的值.
已知函数 .
.
(Ⅰ)求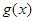 在
在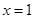 处的切线方程;
处的切线方程;
(Ⅱ)求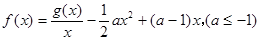 的单调区间;
的单调区间;
(Ⅲ)若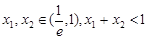 ,求证:
,求证: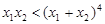 .
.
已知 .
.
(Ⅰ)当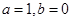 时,判断
时,判断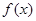 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(Ⅱ)当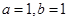 时,若
时,若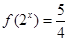 ,求
,求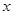 的值;
的值;
(Ⅲ)若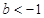 ,且对任何
,且对任何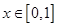 不等式
不等式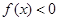 恒成立,求实数
恒成立,求实数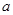 的取值范围.
的取值范围.
某小区在一次对20岁以上居民节能意识的问卷调查中,随机抽取了100份问卷进行统计,得到相关的数据如下表: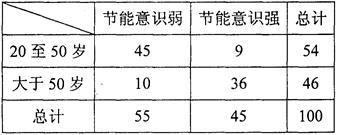
(Ⅰ)由表中数据直观分析,节能意识强弱是否与人的年龄有关?
(Ⅱ)据了解到,全小区节能意识强的人共有350人,估计这350人中,年龄大于50岁的有多少人?
(Ⅲ)按年龄分层抽样,从节能意识强的居民中抽5人,再从这5人中任取2人,求恰有1人年龄在20至50岁的概率.
已知 的内角A、B、C所对的边为
的内角A、B、C所对的边为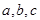 ,
, 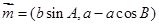 ,
, 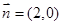 ,且
,且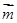 与
与 所成角为
所成角为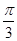 .
.
(Ⅰ)求角B的大小;
(Ⅱ)求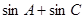 的取值范围.
的取值范围.