(本小题满分12分)
已知各项都不相等的等差数列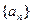 的前六项和为60,且
的前六项和为60,且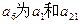 的等比中项.
的等比中项.
(I)求数列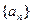 的通项公式
的通项公式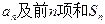 ;
;
(II)若数列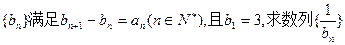 的前n项和Tn.
的前n项和Tn.
如图,在四棱锥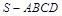 中,平面
中,平面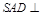 平面
平面 .底面
.底面 为矩形,
为矩形, 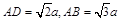 ,
,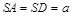 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角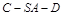 的大小.
的大小.
数列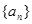 的前
的前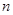 项和记为
项和记为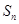 ,
, ,点
,点 在直线
在直线 上,
上, .
.
(Ⅰ)当实数 为何值时,数列
为何值时,数列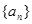 是等比数列?
是等比数列?
(Ⅱ)在(Ⅰ)的结论下,设 ,
,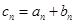 ,
, 是数列
是数列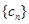 的前
的前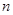 项和,求
项和,求 。
。
如图,在△ABC中,已知B=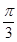 ,AC=4
,AC=4 ,D为BC边上一点.
,D为BC边上一点.
(I)若AD=2,S△ABC=2 ,求DC的长;
,求DC的长;
(Ⅱ)若AB=AD,试求△ADC的周长的最大值.
(本小题满分14分)
已知函数f(x)= x
x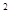 -ax + (a-1)
-ax + (a-1)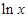 ,
,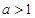 .
.
(I)讨论函数 的单调性;
的单调性;
(II)若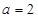 ,数列
,数列 满足
满足 .
.
若首项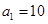 ,证明数列
,证明数列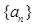 为递增数列;
为递增数列;
若首项为正整数,数列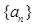 递增,求首项的最小值.
递增,求首项的最小值.
(本小题满分12分)
有甲、乙两种相互独立的预防措施可以降低某地区某灾情的发生.单独采用甲、乙预防措施后,灾情发生的概率分别为0.08和0.10,且各需要费用60万元和50万元.在不采取任何预防措施的情况下发生灾情的概率为0.3.如果灾情发生,将会造成800万元的损失.(设总费用=采取预防措施的费用+可能发生灾情损失费用)
(I)若预防方案允许甲、乙两种预防措施单独采用,他们各自总费用是多少?
(II)若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少的那个方案.