本题满分12分)
某超市为促销商品,特举办“购物有奖100%中奖”活动,凡消费者在该超市购物满10元,可获得一次摇奖机会,购物满20元,可获得两次摇奖机会,以此类推,摇奖机结构如图,将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落,小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中,落入A袋为一等奖,奖金2元,落入B袋为二等奖,奖金1元,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是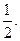
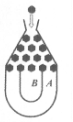
(I)求摇奖两次均获得一等奖的概率;
(II)某消费者购物满20元,摇奖后所得奖金为X元,试求X的分布列与期望;
(III)若超市同时举行购物八八折让利于消费者活动(打折后不能再参加摇奖),某消费者刚好消费20元,请问他是选择摇奖还是选择打折比较划算。
甲乙两位同学参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由;
(3)若将频率视为概率,对甲同学在今后的3次数学竞赛成绩进行预测,记这3次成绩中高于80分的次数为X,求X的分布列及数学期望 。
。
甲、乙两人各射击一次,击中目标的概率分别是 和
和 。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
。假设两人射击是否击中目标,相互之间没有影响;每次射击是否击中目标,相互之间没有影响。
(Ⅰ)求甲射击4次,至少1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设连续两次未击中目标,则停止射击。问:乙恰好射击5次后,被中止射击的概率是多少?
某高级中学共有3000名学生,各年级男、女生人数如下表:
| 高一 |
高二 |
高三 |
|
| 女生 |
523 |
x |
y |
| 男生 |
487 |
490 |
z |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.17.
(1)问高二年级有多少名女生?
(2)现对各年级用分层抽样的方法在全校抽取300名学生,问应在高三年级抽取多少名学生?
已知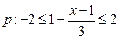 ,
,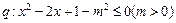 ,且
,且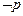 是
是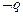 的必要不充分条件,求实数
的必要不充分条件,求实数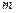 的取值范围.
的取值范围.
8分)
已知集合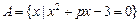 ,集合
,集合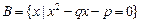 ,且
,且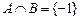 ,求
,求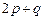 的值.
的值.