(本小题满分12分)在数列 .
.
(1)求证:数列 是等差数列,并求数列
是等差数列,并求数列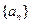 的通项公式
的通项公式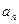 ;
;
(2)设 ,数列
,数列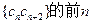 项和为
项和为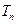 ,是否存在正整整m,使得
,是否存在正整整m,使得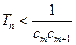 对于
对于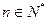 恒成立,若存在,求出m的最小值,若不存在,说明理由.
恒成立,若存在,求出m的最小值,若不存在,说明理由.
在 中,
中, 分别为内角
分别为内角 的对边,满足
的对边,满足 .
.
(1)求A的大小;
(2)若 ,试求内角B、C的大小.
,试求内角B、C的大小.
已知函数 .
.
(1)求函数 的最小值;
的最小值;
(2)已知 ,命题
,命题 :关于
:关于 的不等式
的不等式 对任意
对任意 恒成立;
恒成立; :函数
:函数 是增函数.若“
是增函数.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知函数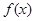 =
=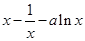 (
( ).
).
(1)若 在点
在点 处的切线与圆
处的切线与圆 相切,求
相切,求 的值;
的值;
(2)是否存在实数 ,使得
,使得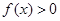 在
在 上恒成立?如果存在,试实数
上恒成立?如果存在,试实数 的取值范围;如果不存在,请说明理由.
的取值范围;如果不存在,请说明理由.
已知函数 =
= .
.
(1)求函数 的单调区间;
的单调区间;
(2)若函数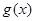 =
= 在[-2,
在[-2, ]恰有2解,求实数
]恰有2解,求实数 的取值范围.
的取值范围.
已知数列{ }是等差数列,
}是等差数列, =4,其前10项和
=4,其前10项和 =100,数列{
=100,数列{ }满足
}满足 =
=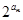 .
.
(1)求数列{ }、数列{
}、数列{ }的通项公式;
}的通项公式;
(2)设 ,求数列{
,求数列{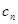 }的前n项和
}的前n项和 .
.