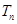设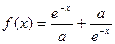 是定义在R上的函数
是定义在R上的函数
(1)f(x)可能是奇函数吗?
(2)当a=1时,试研究f(x)的单调性
(本小题满分10分) 选修4—4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与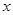 轴的正半轴重合,直线
轴的正半轴重合,直线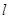 的极坐标方程为:
的极坐标方程为: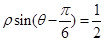 ,曲线
,曲线 的参数方程为:
的参数方程为:
(Ⅰ)写出直线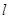 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求曲线 上的点到直线
上的点到直线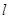 的距离的最大值.
的距离的最大值.
(本小题满分12分)已知椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线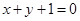 与以椭圆
与以椭圆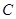 的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆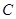 的方程;
的方程;
(Ⅱ)设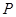 为椭圆
为椭圆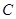 上一点,若过点
上一点,若过点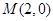 的直线
的直线 与椭圆
与椭圆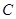 相交于不同的两点
相交于不同的两点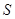 和
和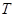 ,满足
,满足 (
(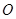 为坐标原点),求实数
为坐标原点),求实数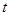 的取值范围.
的取值范围.
(本小题满分12分)如图,已知四棱锥 的底面为菱形,
的底面为菱形, ,
,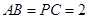 ,
, .
.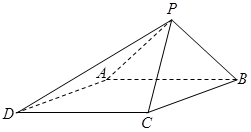
(Ⅰ)求证: ;
;
(Ⅱ)求二面角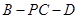 的余弦值.
的余弦值.
(本小题满分12分)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球自由下落,小球在下落的过程中,将遇到黑色障碍物 次,最后落入
次,最后落入 袋或
袋或 袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是
袋中.已知小球每次遇到障碍物时,向左、右两边下落的概率分别是

(Ⅰ)分别求出小球落入 袋和
袋和 袋中的概率;
袋中的概率;
(Ⅱ)在容器的入口处依次放入 个小球,记
个小球,记 为落入
为落入 袋中的小球个数,求
袋中的小球个数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知正项等差数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
,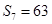 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列 满足
满足 ,
,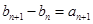 ,求数列
,求数列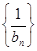 的前
的前 项和
项和