如图,在矩形ABCD中,AB=2,BC=a,又PA⊥平面ABCD,PA=4.
(Ⅰ)若在边BC上存在一点Q,使PQ⊥QD,求a的取值范围;
(Ⅱ)当边BC上存在唯一点Q,使PQ⊥QD时,求二面角A-PD-Q的余弦值.
如图示,在底面为直角梯形的四棱椎P ABCD中,AD//BC,ÐABC= 900, PA^平面ABCD,PA= 4,AD= 2,AB=2 ,BC = 6.
,BC = 6.
(1)求证:BD^平面PAC ;
(2)求二面角A—PC—D的正切值;
(3)求点D到平面PBC的距离.
如图所示,在圆锥PO中, PO= ,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.
,ʘO的直径AB=2, C为弧AB的中点,D为AC的中点.
(1)求证:平面POD^平面PAC;
(2)求二面角B—PA—C的余弦值.
一个多面体的直观图、正视图、侧视图、俯视图如图所示,M、N分别为A1B、B1C1的中点.
(1)求证:MN//平面ACC1A1;
(2)求证:MN^平面A1BC.
解答下列问题:
(1)求平行于直线3x+4y-2=0,且与它的距离是1的直线方程;
(2)求垂直于直线x+3y-5=0且与点P(-1,0)的距离是 的直线方程.
的直线方程.
已知函数 .
.
(1)求函数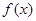 的单调区间;
的单调区间;
(2)若函数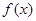 满足:
满足:
①对任意的 ,
, ,当
,当 时,有
时,有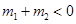 成立;
成立;
②对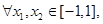
 恒成立.求实数
恒成立.求实数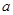 的取值范围.
的取值范围.