如图,已知四棱锥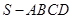 中,
中, 是边长为
是边长为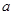 的正三角形,平面
的正三角形,平面 平面
平面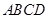 ,四边形
,四边形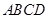 是菱形,
是菱形, ,
, 是
是 的中点,
的中点, 是
是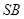 的中点.
的中点.
(1)求证: 平面
平面 .
.
(2)求二面角 的余弦值.
的余弦值.
(本小题满分7分) 选修4-4:坐标系与参数方程
平面直角坐标系中,直线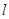 的参数方程是
的参数方程是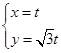 (
(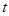 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,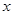 轴的正半轴为极轴,建立极坐标系,已知曲线
轴的正半轴为极轴,建立极坐标系,已知曲线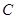 的极坐标方程为
的极坐标方程为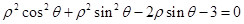 .
.
(Ⅰ)求直线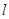 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线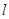 与曲线
与曲线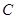 相交于
相交于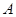 、
、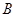 两点,求
两点,求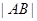 .
.
(本小题满分7分)选修4-2:矩阵与变换
二阶矩阵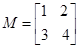 ;
;
(Ⅰ)求点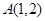 在变换
在变换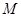 作用下得到的点
作用下得到的点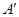 ;
;
(Ⅱ)设直线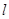 在变换
在变换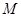 作用下得到了直线
作用下得到了直线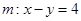 ,求点
,求点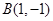 到直线
到直线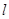 的距离.
的距离.
(本小题满分14分)已知函数 (
(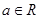 且
且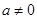 ),
),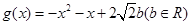 .
.
(Ⅰ)若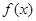 在定义域上有极值,求实数
在定义域上有极值,求实数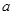 的取值范围;
的取值范围;
(Ⅱ)当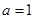 时,若对
时,若对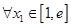 ,总
,总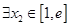 ,使得
,使得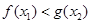 ,求实数
,求实数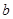 的取值范围;(其中
的取值范围;(其中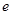 为自然对数的底数);
为自然对数的底数);
(Ⅲ)对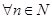 ,且
,且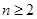 ,证明:
,证明: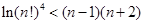 .
.
(本小题满分13分)设椭圆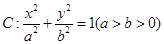 的左、右焦点分别为
的左、右焦点分别为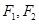 ,上顶点为
,上顶点为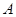 ,在
,在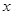 轴负半轴上有一点
轴负半轴上有一点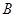 ,满足
,满足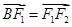 ,
, 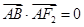 ,且
,且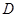 是过
是过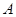 、
、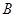 、
、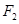 三点的圆上的点,
三点的圆上的点,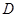 到直线
到直线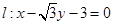 的最大距离等于椭圆长轴的长,求椭圆
的最大距离等于椭圆长轴的长,求椭圆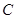 的方程;
的方程;
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若过右焦点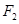 作斜率为
作斜率为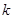 的直线
的直线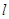 与椭圆
与椭圆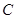 交于
交于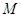 、
、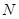 两点,线段
两点,线段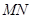 的中垂线与
的中垂线与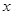 轴相交于点
轴相交于点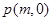 ,求实数
,求实数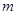 的取值范围.
的取值范围.
(本小题满分13分)正方形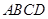 的边长为
的边长为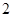 ,
,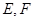 分别为边
分别为边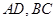 的中点,
的中点,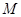 是线段
是线段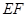 的中点,如图,把正方形沿
的中点,如图,把正方形沿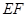 折起,设
折起,设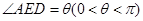 .
.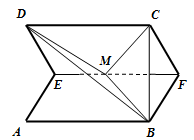
(Ⅰ)求证:无论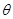 取何值,
取何值,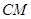 与
与 不可能垂直;
不可能垂直;
(Ⅱ)设二面角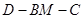 的大小为
的大小为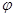 ,当
,当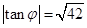 时,求
时,求 的值.
的值.