(本小题满分8分)A、B两城相距100km,在两地之间距A城xkm处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(Ⅰ)把月供电总费用y表示成x的函数,并求定义域;
(Ⅱ)核电站建在距A城多远,才能使供电费用最小.
椭圆C的中心在原点,焦点在x轴上,两焦点F1,F2之间的距离为2 ,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
,椭圆上第一象限内的点P满足PF1⊥PF2,且△PF1F2的面积为1.
(1)求椭圆C的标准方程;
(2)若椭圆C的右顶点为A,直线l:y=kx+m(k≠0)与椭圆C交于不同的两点M,N,且满足AM⊥AN.求证:直线l过定点,并求出定点的坐标.
已知圆C:(x-4)2+(y-m)2=16(m∈N*),直线4x-3y-16=0过椭圆E: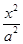 +
+ =1(a>b>0)的右焦点,且被圆C所截得的弦长为
=1(a>b>0)的右焦点,且被圆C所截得的弦长为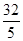 ,点A(3,1)在椭圆E上.
,点A(3,1)在椭圆E上.
(1)求m的值及椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求 ·
·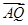 的取值范围.
的取值范围.
已知△ABC的周长为12,顶点A,B的坐标分别为(-2,0),(2,0),C为动点.
(1)求动点C的轨迹E的方程;
(2)过原点作两条关于y轴对称的直线(不与坐标轴重合),使它们分别与曲线E交于两点,求四点所对应的四边形的面积的最大值.
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= ,|AF2|=
,|AF2|=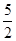 .
.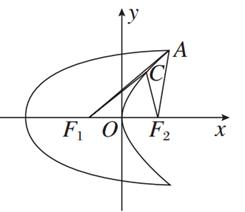
(1)求曲线C1和C2的方程;
(2)设点C是C2上一点,若|CF1|=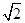 |CF2|,求△CF1F2的面积.
|CF2|,求△CF1F2的面积.
设M、N为抛物线C:y=x2上的两个动点,过M、N分别作抛物线C的切线l1、l2,与x轴分别交于A、B两点,且l1与l2相交于点P,若|AB|=1.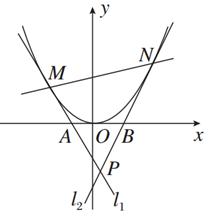
(1)求点P的轨迹方程;
(2)求证:△MNP的面积为一个定值,并求出这个定值.