(本小题满分14分)
已知函数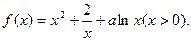
(Ⅰ)若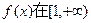 上单调递增,求a的取值范围;
上单调递增,求a的取值范围;
(Ⅱ)若定义在区间D上的函数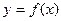 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式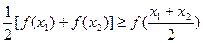 成立,则称函数
成立,则称函数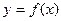 为区间D上的“凹函数”.试判断当
为区间D上的“凹函数”.试判断当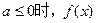 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
一个袋子里有4个不同的红球,6个不同的白球,从中任取4个使得取出的球中红球比白球多的取法有多少种?红球不少于白球的取法又有多少种?
(1)把5本不同的书分给3名同学,每人一本,有多少种不同的分法?
(2)把5本相同的书分给3名同学,每人一本,有多少种不同的分法?
(选修4-5;不等式选讲)若 与不等式
与不等式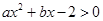 同解,
同解, 的解集为空集,求
的解集为空集,求 的取值范围.
的取值范围.
(选修4-4;坐标系与参数方程)已知直线 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角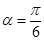 ,
,
(1)写出直线 的参数方程;
的参数方程;
(2)设 与圆
与圆 相交与两点A、B,求点P到A、B两点的距离之积.
相交与两点A、B,求点P到A、B两点的距离之积.
(本小题满分12分)已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1,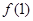 )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在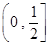 上至少存在一个实数
上至少存在一个实数 ,使
,使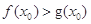 成立,求正实数
成立,求正实数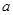 的取值范围.
的取值范围.