(本小题满分1 0分)选修4-1:几何证明选讲
0分)选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C
作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。
(I)求证:DC是⊙O的切线;
(II)求证:AM:MB=DF·DA。
已知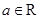 ,函数
,函数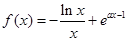 (
(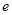 为自然对数的底数).
为自然对数的底数).
(Ⅰ)若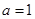 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅱ)若 的最小值为
的最小值为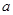 ,求
,求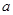 的最小值.
的最小值.
已知椭圆 :
: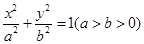 的左焦点
的左焦点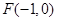 ,离心率为
,离心率为 ,函数
,函数
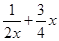 ,
,
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)设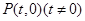 ,
,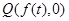 ,过
,过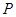 的直线
的直线 交椭圆
交椭圆 于
于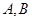 两点,求
两点,求 的最小值,并求此时的
的最小值,并求此时的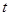 的值.
的值.
如图,在四棱锥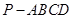 中,四边形
中,四边形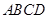 是正方形,
是正方形,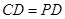 ,
,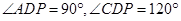 ,
,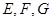 分别为
分别为 的中点.
的中点.
(Ⅰ)求证:平面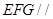 平面
平面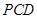 ;
;
(Ⅱ)求二面角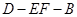 的平面角的大小.
的平面角的大小.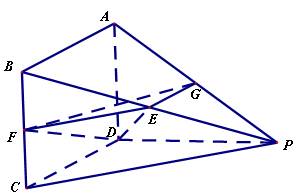
数列{an}中,an>0,an≠1,且 (n∈N*).
(n∈N*).
(1)证明:an≠an+1;
(2)若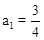 ,计算a2,a3,a4的值,并求出数列{an}的通项公式.
,计算a2,a3,a4的值,并求出数列{an}的通项公式.
已知函数 (
(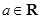 ,
,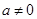 ),
),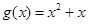 .
.
(1)求函数 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数;
(2)若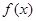 在其定义域内单调递增,求
在其定义域内单调递增,求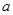 的取值范围;
的取值范围;
(3)证明不等式 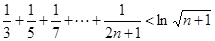 (
( ).
).