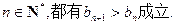棱长为2的正方体A1B1C1D1-ABCD中,E、F分别是C1C和D1A1的中点,
(1)求异面直线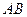 与
与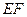 所成的角的余弦值;
所成的角的余弦值;
(2)求点A到EF的距离.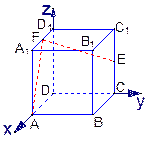
(1)设函数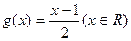 ,且数列
,且数列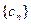 满足
满足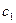 = 1,
= 1,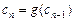 (n∈N,
(n∈N,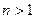 );求数列
);求数列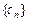 的通项公式.
的通项公式.
(2)设等差数列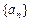 、
、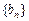 的前n项和分别为
的前n项和分别为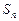 和
和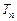 ,且
,且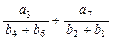
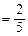 ,
,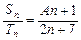 ,
, 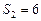 ;求常数A的值及
;求常数A的值及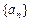 的通项公式.
的通项公式.
(3)若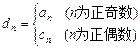 ,其中
,其中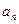 、
、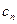 即为(1)、(2)中的数列
即为(1)、(2)中的数列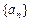 、
、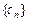 的第
的第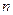 项,试求
项,试求
(本小题满分12分)已知函数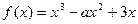
(1)若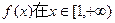 上增函数,求实数a的取值范围;
上增函数,求实数a的取值范围;
(2)若x=3是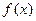 的极值点,求
的极值点,求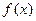 在
在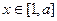 上的最小值和最大值.
上的最小值和最大值.
(本小题满分12分)已知△ABC中,A、B、C所对的边分别为a、b、c,当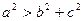 且
且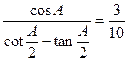 时,求sin2A的值.
时,求sin2A的值.
(本小题满分14分)
设数列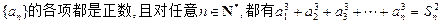 ,
,
其中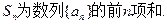
(I)求证: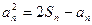 ;
;
(II)求数列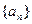 的通项公式;
的通项公式;
(III)设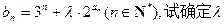 的取值范围,使得对任意
的取值范围,使得对任意