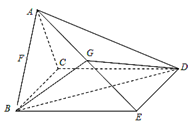
如图，四棱锥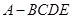，平面⊥平面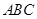，△是边长为2的等边三角形，底面是矩-优题课

如图，四棱锥，平面⊥平面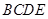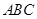，△是边长为2的等边三角形，底面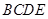是矩形，且．

（1）若点是的中点，求证：平面；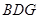
（2）试问点在线段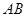上什么位置时，二面角的大小为．

科目数学题型解答题难度中等

知识点：平行线法

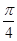为了研究一种新药的疗效，选100名患者随机分成两组，每组各 $50$ 名，一组服药，另一组不服药．一段时间后，记录了两组患者的生理指标 $x$ 和 $y$ 的数据，并制成如图，其中“*”表示服药者，“+”表示未服药者．

（1）从服药的50名患者中随机选出一人，求此人指标 $y$ 的值小于 $60$ 的概率；

（2）从图中A，B，C，D四人中随机选出两人，记 $ξ$ 为选出的两人中指标x的值大于1.7的人数，求 $ξ$ 的分布列和数学期望 $E （ ξ ）$ ；

（3）试判断这100名患者中服药者指标 $y$ 数据的方差与未服药者指标y数据的方差的大小．（只需写出结论）

如图，在四棱锥 $P ﹣ ABCD$ 中，底面 $ABCD$ 为正方形，平面 $PAD ⊥$ 平面 $ABCD$ ，点M在线段PB上， $PD ∥$ 平面 $MAC$ ， $PA = PD = \sqrt{6}$ ， $AB = 4$ ．

（1）求证：M为PB的中点；

（2）求二面角 $B ﹣ PD ﹣ A$ 的大小；

（3）求直线MC与平面BDP所成角的正弦值．

在 $△ ABC$ 中， $∠ A = 60 °$ ， $c = \frac{3}{7} a$ ．

（1）求 $sinC$ 的值；

（2）若 $a = 7$ ，求 $△ ABC$ 的面积．

给定无穷数列 ${a_{n}}$ ，若无穷数列{b _n}满足：对任意 $n \in N *$ ，都有 $| b_{n} - a_{n} | \leq 1$ ，则称 ${b_{n}} 与 {a_{n}}$ "接近"。

（1）设 ${a_{n}}$ 是首项为1，公比为 $\frac{1}{2}$ 的等比数列， $b_{n} = a_{n + 1} + 1$ ， $n \in N *$ ，判断数列 ${b_{n}}$ 是否与 ${a_{n}}$ 接近，并说明理由；

（2）设数列 ${a_{n}}$ 的前四项为： $a_{1}$ =1， $a_{2}$ =2， $a_{3}$ =4， $a_{4}$ =8， $\{b_{n}\}$ 是一个与 ${a_{n}}$ 接近的数列，记集合M={x|x=b _i， i=1，2，3，4}，求M中元素的个数m；

（3）已知 ${a_{n}}$ 是公差为d的等差数列，若存在数列{b _n}满足：{b _n}与 ${a_{n}}$ 接近，且在b₂-b₁，b₃-b₂，…b ₂₀₁-b ₂₀₀中至少有100个为正数，求d的取值范围。

设常数 $t > 2$ ，在平面直角坐标系xOy中，已知点F（2，0），直线 $l$ ： $x = t$ ，曲线 $Γ$ ： $y ² = 8 x (0 \leq x \leq t ， y \geq 0)$ ， $l$ 与x轴交于点A，与 $Γ$ 交于点B，P、Q分别是曲线 $Γ$ 与线段AB上的动点。

（1）用t表示点B到点F的距离；

（2）设t=3， $∣ FQ ∣ = 2$ ，线段OQ的中点在直线FP上，求△AQP的面积；

（3）设t=8，是否存在以FP、FQ为邻边的矩形FPEQ，使得点E在 $Γ$ 上？若存在，求点P的坐标；若不存在，说明理由。

试卷网试题网古诗词网作文网范文网