一快餐店试销某种套餐,试销一段时间后发现,每份套餐的成本为5元,该店每天固定支出费用为600元(不含套餐成本).若每份售价不超过10元,每天可销售400份;若每份售价超过10元,每提高1元,每天的销售量就减少40份.为了便于结算,每份套餐的售价x(元)取整数,用y(元)表示该店日净收入.(日净收入=每天的销售额-套餐成本-每天固定支出)
(1)求y与x的函数关系式;
(2)若每份套餐售价不超过10元,要使该店日净收入不少于800元,那么每份售价最少不低于多少元?
(3)该店既要吸引顾客,使每天销售量较大,又要有较高的日净收入.按此要求,每份套餐的售价应定为多少元?此时日净收入为多少?
如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(0,4),B(﹣3,5),C(﹣4,1).
(1)把△ABC向右平移2个单位得△A1B1C1,请画出△A1B1C1,并写出点A1的坐标;
(2)把△ABC绕原点O旋转180°得到△A2B2C2,请画出△A2B2C2.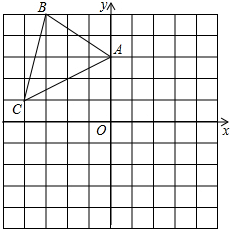
如图,已知∠1=36°,当∠2等于多少度时,AB∥CD?请说明理由.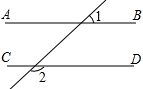
如图,∠1=∠2,AC平分∠DAB,求证:DC∥AB.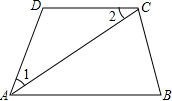
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.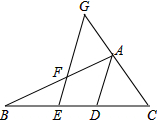
看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
解:∵∠1=35°,∠2=35°(已知),
∴∠1=∠2
∴_______∥_______(同位角相等,两条直线平行)
又∵AC⊥AE(已知),
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=_______°(等式的性质)
同理可得,∠FBD+∠2=_______°
∴_______∥_______(同位角相等,两条直线平行)