(本小题满分12分)
已知双曲线 的离心率为
的离心率为 ,右准线方程为
,右准线方程为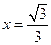
(Ⅰ)求双曲线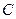 的方程;
的方程;
(Ⅱ)设直线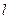 是圆
是圆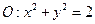 上动点
上动点 处的切线,
处的切线,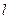 与双曲线
与双曲线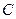 交于不同的两点
交于不同的两点 ,证明
,证明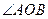 的大小为定值.
的大小为定值.
(本小题满分14分)
已知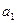 =2,点(
=2,点(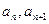 )在函数
)在函数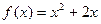 的图像上,其中
的图像上,其中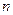 =
=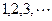 .
.
(1)证明:数列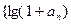 }是等比数列;
}是等比数列;
(2)设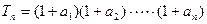 ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式;
(3)记 ,求数列{
,求数列{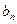 }的前n项和
}的前n项和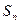 ,并证明
,并证明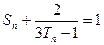 .
.
已知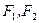 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为坐标原点,点
为坐标原点,点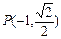 在椭圆上,且
在椭圆上,且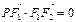 ,⊙
,⊙ 是以
是以 为直径的圆,直线
为直径的圆,直线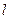 :
: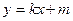 与⊙
与⊙ 相切,并且与椭圆交于不同的两点
相切,并且与椭圆交于不同的两点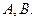
(1)求椭圆的标准方程;
(2)当 ,求
,求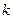 的值.
的值.
((本小题满分12分)
如图,已知在直四棱柱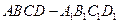 中,
中,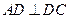 ,
, ,
,
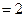 .
.
(1)求证: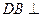 平面
平面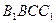 ;
;
(2)求二面角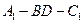 的余弦值.
的余弦值.
((本小题满分12分)
在△ABC中,a,b,c分别为角A,B,C所对的三边,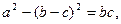
(1)求角A; (2)若BC=2
(2)若BC=2 ,角B等于x,周长为y,求函数
,角B等于x,周长为y,求函数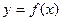 的取值范围.
的取值范围.
(本小题满分12分)
解关于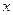 的不等式
的不等式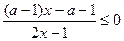
 .
.