(本小题满分12分)在10件产品中,有8件是合格的,2件是次品,从中任意抽2件进行检验.
计算:(1)两件都是次品的概率;
(2)2件中恰好有一件是合格品的概率;
(3)至多有一件是合格品的概率.
如图,四棱锥P—ABCD中,底面ABCD是边长为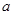 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=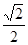 AD.
AD.
(Ⅰ)求证:EF//平面PAD;
(Ⅱ)求三棱锥C—PBD的体积.
已知公比大于1的等比数列{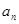 }满足:
}满足: +
+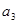 +
+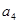 =28,且
=28,且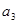 +2是
+2是 和
和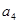 的等差中项.
的等差中项.
(Ⅰ)求数列{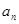 }的通项公式;
}的通项公式;
(Ⅱ)若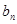 =
=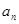
 ,求{
,求{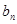 }的前n项和
}的前n项和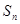 .
.
设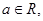 函数
函数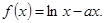
(I)求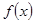 的单调区间;
的单调区间;
(II)若函数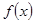 无零点,求实数
无零点,求实数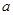 的取值范围.
的取值范围.
设平面内两定点 、
、 ,直线
,直线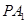 和
和 相交于点
相交于点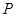 ,且它们的斜率之积为定值
,且它们的斜率之积为定值 。
。
(I)求动点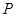 的轨迹
的轨迹 的方程;
的方程;
(II)设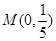 ,过点
,过点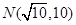 作抛物线
作抛物线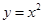 的切线交曲线
的切线交曲线 于
于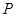 、
、 两点,求
两点,求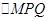 的面积。
的面积。
某项新技术进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测。假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
(Ⅰ)求该项技术量化得分不低于8分的概率;
(Ⅱ)记该技术的三个指标中被检测合格的指标个数为随机变量 ,求
,求 的分布列与数学期望。
的分布列与数学期望。