（本小题共13分）直线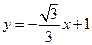
和
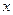轴，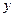
轴分别交于点
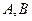，以线段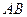
为边在第一象限内作等边△
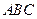，如果在第一象限内有一点
使得△
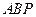和△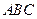的面积相等， 求
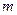的值。
已知
且
（1）求
的值；
（2）求
的值；
已知幂函数
的图象与x轴，y轴无交点且关于原点对称，又有函数f(x)=x2－alnx+m－2在(1，2]上是增函数，g(x)=x－
在(0,1)上为减函数.
①求a的值；
②若
，数列{an}满足a1＝1，an+1＝p(an)，（n∈N+），数列{bn}，满足
，
，求数列{an}的通项公式an和sn.
③设
，试比较[h(x)]n+2与h(xn)+2n的大小（n∈N+），并说明理由.
已知二次函数h(x)=ax2+bx+c(其中c<3)，其导函数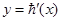
的图象如图，f(x)=6lnx+h(x).
①求f(x)在x=3处的切线斜率；
②若f(x)在区间(m,m+
)上是单调函数，求实数m的取值范围；
③若对任意k∈[-1,1]，函数y=kx(x∈(0,6])的图象总在函数y＝f(x)图象的上方，求c的取值范围.
仔细阅读下面问题的解法：
设A＝[0，1]，若不等式21－x+a>0在A上有解，求实数a的取值范围.
解：令f(x)＝21－x+a，因为f(x)>0在A上有解。
＝2+a>0
a>-2
学习以上问题的解法，解决下面的问题，已知：函数f(x)=x2+2x+3(-2≤x≤-1).
①求f(x)的反函数f-1(x)及反函数的定义域A；
②设B＝
，若A∩B≠
,求实数a的取值范围.
若f(x)的定义域为[a,b]，值域为[a,b]（a<b），则称函数f(x)是[a,b]上的“四维光军”函数.
①设g(x)＝
x2－x+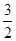
是[1，b]上的“四维光军”函数，求常数b的值;
②问是否存在常数a，b（a>－2），使函数h(x)=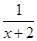
是区间[a,b]上的“四维光军”函数？若存在，求出a,b的值，否则，请说明理由.