（本小题满分10分）通过点A（0，a）的直线
与圆
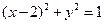相交于不同的两点B、C，在线段BC上取一点P，使
=
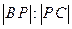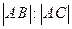，设点B在点C的左边，（1）试用a和k表示P点的坐标；（2）求k变化时P点的轨迹；（3）证明不论a取何值时，上述轨迹恒过圆内的一定点．
（本小题满分12分）设全集为R，集合
，
，
（1）求：
；
（2）若集合
，满足
，求实数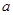
的取值范围。
（本小题满分10分）已知在半径为10的圆O中，弦AB的长为10。
（1）求弦AB所对的圆心角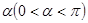
的大小。
（2）求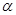
所在的扇形弧长
及弧所在的弓形的面积S。
已知椭圆
的离心率为
，且过点
（1）求椭圆的标准方程：
（2）四边形ABCD的顶点在椭圆上，且对角线AC，BD过原点O，若
①求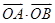
的最值：
②求证：四边形ABCD的面积为定值.
已知圆A：x2＋y2－2x－2y－2＝0.
（1）若直线l：ax＋by－4＝0平分圆A的周长，求原点O到直线l的距离的最大值；
（2）若圆B平分圆A的周长，圆心B在直线y＝2x上，求符合条件且半径最小的圆B的方程．
如图，将边长为2，有一个锐角为60°的菱形
，沿着较短的对角线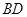
对折，使得
，
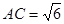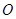为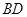的中点.若P为AC上的点，且满足
。
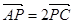（Ⅰ）求证：
（Ⅱ）求三棱锥
的体积；