解下列方程(每小题5分,共10分)
①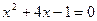 . ②
. ②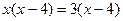
如图,矩形ABCD中,AB=4cm,AD="3" cm,点P从A点出发,以5cm/s的速度,沿AC向C作匀速运动;与此同时,点Q也从A点出发,以4cm/s的速度,沿射线AB作匀速运动。当P运动到C点时,P、Q都停止运动。设点P运动的时间为ts。

(1)当P异于A.C时,证明:以P为圆心、PQ长为半径的圆总是与边AB相切;
(2)在整个运动过程中,t为怎样的值时,以P为圆心、PQ长为半径的圆与边BC分别有1个公共点和2个公共点?
如图,等腰梯形MNPQ的上底长为2,腰长为3,一个底角为60°.正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD在梯形的外面沿边MN、NP、PQ进行翻滚,翻滚到有一个顶点与Q重合即停止滚动.
求正方形在整个翻滚过程中点A所经过的路线与梯形MNPQ的三边MN、NP、PQ所围成图形的面积S.
如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究: 是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,请求出该最大值;若不存在,请说明理由.
如图1,矩形MNPQ中,点E、F、G、H分别在NP、PQ、QM、MN上,若 ,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且
,则称四边形EFGH为矩形MNPQ的反射四边形.在图2、图3中,四边形ABCD为矩形,且 ,
, .
.
(1)在图2、图3中,点E、F分别在BC、CD边上,图2中的四边形EFGH是利用正方形网格在图上画出的矩形ABCD的反射四边形.请你利用正方形网格在图3上画出矩形ABCD的反射四边形EFGH;
(2)图2、图3中矩形ABCD的反射四边形EFGH的周长是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的周长各是多少;
(3)图2、图3中矩形ABCD的反射四边形EFGH的面积是否为定值?若是定值,请直接写出这个定值;若不是定值,请直接写出图2、图3中矩形ABCD的反射四边形EFGH的面积各是多少.
如图,直线l1与x轴、y轴分别交于A、B两点,直线l2与直线l1关于x轴对称,已知直线l1的解析式为 .
.

(1)求直线l2的解析式;
(2)过A点在△ABC的外部作一条直线l3,过点B作BE⊥l3于E,过点C作CF⊥l3于F,请画出图形并求证:BE+CF=EF;
(3)△ABC沿y轴向下平移,AB边交x轴于点P,过P点的直线与AC边的延长线相交于点Q,与y轴相交于点M,且BP=CQ,在△ABC平移的过程中,①OM为定值;②MC为定值.在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值.