(本小题满分16分,第1小题满分6分,第2小题满分10分)
已知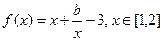
(1) 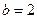 时,求
时,求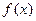 的值域;
的值域;
(2) 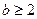 时,
时,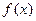 的最大值为M,最小值为m,且满足:
的最大值为M,最小值为m,且满足: ,求b的取值范围.
,求b的取值范围.
设函数 .
.
(1)求 的最小正周期和值域;
的最小正周期和值域;
(2)在锐角△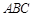 中,角
中,角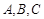 的对边分别为
的对边分别为 ,若
,若 且
且 ,
,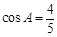 ,求
,求 和
和 .
.
设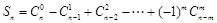 ,
, 且
且 ,其中当
,其中当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时,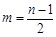 .
.
(1)证明:当 ,
,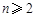 时,
时,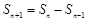 ;
;
(2)记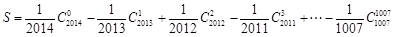 ,求
,求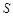 的值.
的值.
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 的分布列和数学期望.
的分布列和数学期望.
已知函数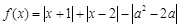 ,若函数
,若函数 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数 的取值范围.
的取值范围.
在平面直角坐标系 中,圆的参数方程为
中,圆的参数方程为 ,以坐标原点
,以坐标原点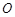 为极点,
为极点, 轴的正半轴为极轴建立极坐标系.求:
轴的正半轴为极轴建立极坐标系.求:
(1)圆的直角坐标方程;
(2)圆的极坐标方程.