(本小题满分12分)
已知函数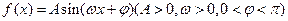 的一个周期的图象,如图(1)求
的一个周期的图象,如图(1)求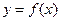 的解析式(2)若函数
的解析式(2)若函数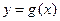 与
与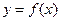 的图象关于直线
的图象关于直线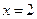 对称,求
对称,求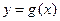 的解析式.
的解析式.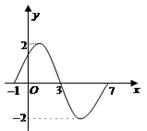
(本小题满分10分,几何证明选讲)
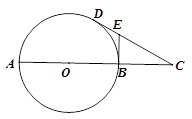
如图,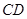 是圆
是圆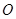 的切线,切点为
的切线,切点为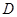 ,
,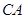 是过圆心的割线且交圆
是过圆心的割线且交圆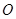 于
于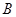 点,过
点,过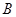 作
作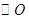 的切线交
的切线交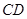 于点
于点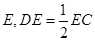 .
.
求证:(1)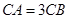 ;(2)
;(2)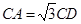 .
.
己知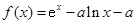 ,其中常数
,其中常数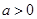 .
.
(1)当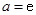 时,求函数
时,求函数 的极值;
的极值;
(2)若函数 有两个零点
有两个零点 ,求证:
,求证: ;
;
(3)求证: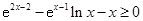 .
.
已知 ,
, ,
, 都是各项不为零的数列,且满足
都是各项不为零的数列,且满足 ,
, ,其中
,其中 是数列
是数列 的前
的前 项和,
项和,  是公差为
是公差为 的等差数列.
的等差数列.
(1)若数列 是常数列,
是常数列, ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(2)若 (
( 是不为零的常数),求证:数列
是不为零的常数),求证:数列 是等差数列;
是等差数列;
(3)若 (
( 为常数,
为常数, ),
),
 ,求证:对任意的
,求证:对任意的 ,数列
,数列 单调递减.
单调递减.
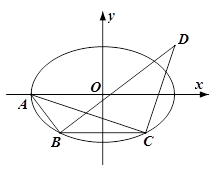
如图,在平面直角坐标系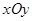 中,椭圆
中,椭圆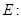
 的左顶点为
的左顶点为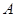 ,与
,与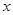 轴平行的直线与椭圆
轴平行的直线与椭圆 交于
交于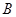 、
、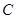 两点,过
两点,过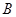 、
、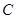 两点且分别与直线
两点且分别与直线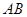 、
、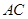 垂直的直线相交于点
垂直的直线相交于点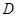 .已知椭圆
.已知椭圆 的离心率为
的离心率为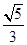 ,右焦点到右准线的距离为
,右焦点到右准线的距离为 .
. 
(1)求椭圆 的标准方程;
的标准方程;
(2)证明点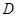 在一条定直线上运动,并求出该直线的方程;
在一条定直线上运动,并求出该直线的方程;
(3)求 面积的最大值.
面积的最大值.
如图,某市有一条东西走向的公路 ,现欲经过公路
,现欲经过公路 上的
上的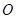 处铺设一条南北走向的公路
处铺设一条南北走向的公路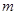 .在施工过程中发现在
.在施工过程中发现在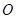 处的正北
处的正北 百米的
百米的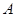 处有一汉代古迹.为了保护古迹,该市决定以
处有一汉代古迹.为了保护古迹,该市决定以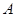 为圆心,
为圆心, 百米为半径设立一个圆形保护区.为了连通公路
百米为半径设立一个圆形保护区.为了连通公路 、
、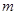 ,欲再新建一条公路
,欲再新建一条公路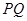 ,点
,点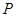 、
、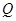 分别在公路
分别在公路 、
、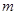 上,且要求
上,且要求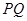 与圆
与圆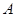 相切.
相切.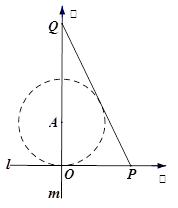
(1)当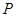 距
距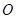 处
处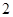 百米时,求
百米时,求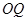 的长;
的长;
(2)当公路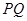 长最短时,求
长最短时,求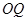 的长.
的长.