(本小题满分12分)
四 棱锥
棱锥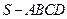 的底面
的底面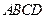 是
是 正方形,侧棱
正方形,侧棱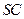 的中点
的中点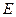 在底面内的射影恰好是正方形
在底面内的射影恰好是正方形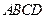 的中心
的中心 ,
, 顶点
顶点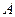 在截面
在截面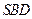 内
内 的射影恰好是
的射影恰好是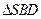 的重心
的重心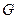 .
.
(1)求直线 与底面
与底面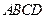 所成角的正切值;
所成角的正切值;
(2)设 ,求此四棱锥过点
,求此四棱锥过点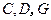 的截面面积.
的截面面积.
如图,在平行四边形 中,
中, ,
, ,
, 为线段
为线段 的中线,将△
的中线,将△ 沿
沿 直线
直线 翻折成△
翻折成△ ,使平面
,使平面 ⊥平面
⊥平面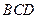 ,
,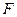 为线
为线 段
段 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)设 为线段
为线段 的中点,求直线
的中点,求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知一隧道的截面 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽 米,车高
米,车高 米.
米.
(1)若此隧道为单向通行,经测量隧道的跨度是 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行?
(2)圆可以看作是长轴短轴相等的特殊椭圆,类比圆面积公式,
请你推测椭圆 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
求经过点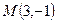 ,且与圆
,且与圆 相切于点
相切于点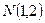 的圆
的圆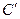 的方程,并判断两圆是外切还是内切?
的方程,并判断两圆是外切还是内切?
直线 经过点
经过点 ,且与圆
,且与圆 相交与
相交与 两点,截得的弦长为
两点,截得的弦长为 ,求
,求 的方程?
的方程?
已知直线 :
: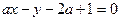
⑴求证:不论实数取何值,直线 总经过第一
总经过第一 象限
象限
⑵为使直线不经过第二象限,求实数 的取值范围
的取值范围