每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
按类用分层抽样的方法在这个月生产的 轿车中抽取50辆,其中有A类轿车10辆
轿车中抽取50辆,其中有A类轿车10辆 .
.
(Ⅰ)求z的值.
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将 该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
| |
轿车A |
轿车B |
轿 车C 车C |
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
已知△ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2+bc,求:(1) 2sinBcosC﹣sin(B﹣C)的值;(2)若a=2,求△ABC周长的最大值.
抛物线y2=2px(p>0)上纵坐标为-p的点M到焦点的距离为2.
(1)求p的值;
(2)如图,A,B,C为抛物线上三点,且线段MA,MB,MC 与x轴交点的横坐标依次组成公差为1的等差数列,若△AMB的面积是△BMC面积的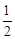 ,求直线MB的方程.
,求直线MB的方程.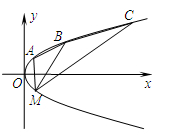
已知函数
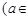 R).
R).
(1)若 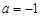 ,求曲线
,求曲线 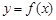 在点
在点 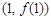 处的的切线方程;
处的的切线方程;
(2)若 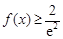 对任意
对任意 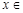
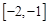 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
| 日需求量n |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 频数 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
(1)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
(2)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
已知数列 {an} 是首项为 a1=1 的等差数列,其前n项和为Sn,数列 {bn} 是首项 b1=2 的等比数列,且 b2S2=16,b1b3=b4.
(1)求数列 {an},{bn} 的通项公式;
(2)若数列 {cn} 满足 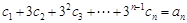 ,求数列 {cn} 的前n项和 Tn.
,求数列 {cn} 的前n项和 Tn.