(本小题满分12分)

 某体育馆拟用运动场的边角地建一个矩形的健身室
某体育馆拟用运动场的边角地建一个矩形的健身室 (如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
(如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
(本小题满分12分)二次函数f(x)满足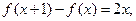 且f(0)=1.
且f(0)=1.
(1)求f(x)的解析式;
(2)在区间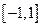 上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
上,y= f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
(本小题满分12分)判断y=1-2x3在(-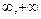 )上的单调性,并用定义证明。
)上的单调性,并用定义证明。
(本小题满分14分)设二次函数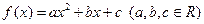 满足下列条件:
满足下列条件:
①当 ∈R时,
∈R时,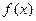 的最小值为0,且f (
的最小值为0,且f ( -1)=f(-
-1)=f(- -1)成立;
-1)成立;
②当 ∈(0,5)时,
∈(0,5)时, ≤
≤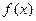 ≤2
≤2 +1恒成立。
+1恒成立。
(1)求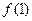 的值;
的值;
(2)求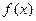 的解析式;
的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当 ∈
∈ 时,就有
时,就有 成立。
成立。
(本小题满分13分)
某出版公司为一本畅销书定价如下: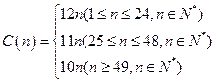 .这里n表示定购书
.这里n表示定购书
的数量,C(n)是定购n本书所付的钱数(单位:元)
(1)有多少个n,会出现买多于n本书比恰好买n本书所花钱少?
(2)若一本书的成本价是5元,现有两人来买书,每人至少买1本,两人共买60本,问出版公司至少能赚多少钱?最多能赚多少钱?
(本题满分12分) 已知函数 的图象与函数
的图象与函数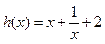 的图象关于点A
的图象关于点A
(0,1)对称.(1)求函数 的解析式(2)若
的解析式(2)若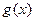 =
= +
+ ,且
,且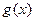 在区间(0,
在区间(0,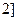
上的值不小于 ,求实数
,求实数 的取值范围.
的取值范围.