(本小题满分12分)
已知向量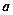
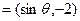 与
与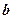
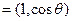 ,其中
,其中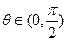 ,且
,且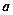
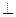
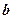 .
.
(1)求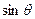 和
和 的值;
的值;
(2)若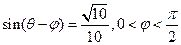 ,求
,求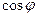 的值.
的值.
已知椭圆
:
的一个顶点为
(2,0),离心率为
,直线
与椭圆
交于不同的两点
。
(1)求椭圆
的方程
(2)当
的面积为
时,求
的值。
已知函数 .
(1)若曲线
与曲线
在它们的交点
处具有公共切线,求
的值
(2)当
时,若函数
在区间
上的最大值为28,求
的取值范围
近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
| "厨余垃圾"箱 |
"可回收物"箱 |
"其他垃圾"箱 |
|
| 厨余垃圾 |
400 |
100 |
100 |
| 可回收物 |
30 |
240 |
30 |
| 其他垃圾 |
20 |
20 |
60 |
(1)试估计厨余垃圾投放正确的概率;
(2)试估计生活垃圾投放错误的概率 ;
(3)假设厨余垃圾在"厨余垃圾"箱、"可回收物"箱、"其他垃圾"箱的投放量分别为
,其中
.当数据
的方差
最大时,写出
的值(结论不要求证明),并求此时
的值.
(注:
,其中
为数据
的平均数)
如图1,在 中, , 别为 的中点,点 为线段 上的一点,将 沿 折起到 的位置,使 ,如图2.
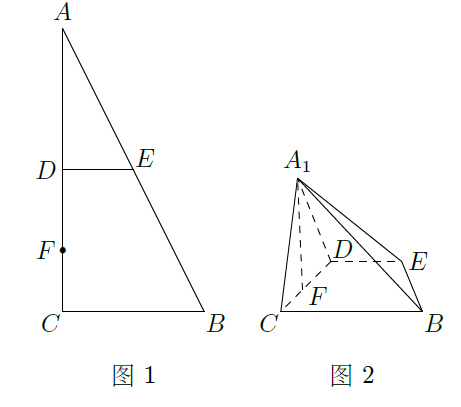
(Ⅰ)求证: 平面 ;
(Ⅱ)求证: (Ⅲ)线段 上是否存在点 ,使 ?说明理由.
已知函数 .
(Ⅰ)求
的定义域及最小正周期
(Ⅱ)求
的单调递减区间。