.(本小题满分12分)
已知:直线AB过圆心O,交⊙O于AB,直线AF交⊙O于AF(不与B重合),直线l与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC。
求证:(1)
(2)AC2=AE·AF。
在平面直角坐标系 O
O 中,直线
中,直线 与抛物线
与抛物线 =2
=2 相交于A、B两点。
相交于A、B两点。
(1)求证:命题“如果直线 过点T(3,0),那么
过点T(3,0),那么 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由。
已知在平面直角坐标系 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为 ,右顶点为
,右顶点为 ,设点
,设点 .
.
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,求线段
是椭圆上的动点,求线段 中点
中点 的轨迹方程;
的轨迹方程;
(3)过原点 的直线交椭圆于点
的直线交椭圆于点 ,求
,求 面积的最大值。
面积的最大值。
已知直线l经过点(0,-2),其倾斜角是60°.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成三角形的面积.
求直线 被圆
被圆 所截得的弦长.
所截得的弦长.
已知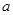 为实数,
为实数,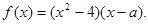
(1)若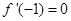 ,求
,求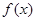 在
在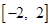 上最大值和最小值;
上最大值和最小值;
(2)若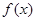 在
在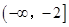 和
和 上都是递增的,求
上都是递增的,求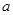 的取值范围。
的取值范围。