(本小题共12分)
设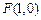 ,
,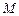 点在
点在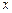 轴的负半轴上,点
轴的负半轴上,点 在
在 轴上,且
轴上,且 .
.
(1)当点 在
在 轴上运动时,求点
轴上运动时,求点 的轨迹
的轨迹 的方程;
的方程;
(2)若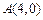 ,是否存在垂直
,是否存在垂直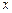 轴的直线
轴的直线 被以
被以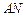 为直径的圆截得的弦长恒为定值?若存在,求出直线
为直径的圆截得的弦长恒为定值?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)已知等比数列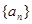 中,
中,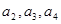 分别是某等差数列的第5项、第3项、第2项,且
分别是某等差数列的第5项、第3项、第2项,且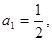 公比
公比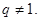
(1)求数列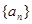 的通项公式;
的通项公式;
(2)已知数列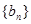 满足:
满足: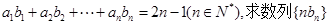 的前n项和
的前n项和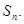
(本小题满分12分)某工厂每天生产某种产品最多不超过40件,并且在生产过程中产品的正品率P与每日生产产品件数x(x∈N*)间的关系为P=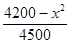 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.(注:正品率=产品的正品件数÷产品总件数×100%).
(Ⅰ)将日利润y(元)表示成日产量x(件)的函数;
(Ⅱ)求该厂的日产量为多少件时,日利润最大?并求出日利润的最大值.
(本小题满分12分)设直线 与椭圆
与椭圆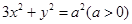 相交于
相交于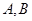 两个不同的点,与
两个不同的点,与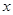 轴相交于点
轴相交于点 ,记
,记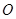 为坐标原点.
为坐标原点.
(1)证明: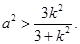
(2)若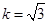 且
且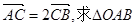 的面积及椭圆方程.
的面积及椭圆方程.
(本小题满分10分)已知命题p:函数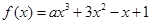 在R上是减函数;命题q:在平面直角坐标系中,点
在R上是减函数;命题q:在平面直角坐标系中,点 在直线
在直线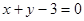 的左下方。若
的左下方。若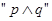 为假,
为假,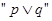 为真,求实数
为真,求实数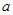 的取值范围
的取值范围
(本小题满分14分)
已知椭圆 的离心率为
的离心率为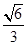 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为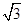 .
.
(1)求椭圆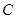 的方程;
的方程;
(2)设直线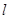 与椭圆
与椭圆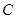 交于
交于 两点,坐标原点
两点,坐标原点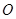 到直线
到直线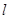 的距离为
的距离为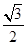 ,求
,求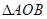
面积的最大值.