(本小题满分14分)
已知数列{an}中，a1＝t(t∈R，且t≠0,1)，a2＝t2，且当x＝t时，
函数f(x)＝(an－an－1)x2－(an＋1－an)x(n≥2，n∈N)取得极值.
(Ⅰ)求证：数列{an＋1－an}是等比数列；
(Ⅱ)若bn＝anln|an|(n∈N)，求数列{bn}的前n项和Sn；
(Ⅲ)当t＝－时，数列{bn}中是否存在最大项？如果存在，说明是第几项；如果不存在，请说明理由.
已知函数
且
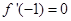
（Ⅰ）试用含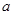
的代数式表示
；
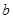（Ⅱ）求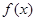
的单调区间；
（Ⅲ）令
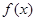，设函数在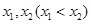
处取得极值，记点
，证明：线段
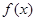与曲线存在异于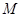
、
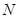的公共点；
已知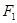
、
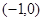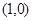为椭圆的焦点，且直线
与椭圆相切．
（Ⅰ）求椭圆方程；
（Ⅱ）过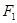的直线交椭圆于
、
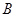两点，求△
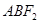的面积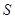
的最大值，并求此时直线的方程。
已知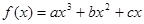
在区间[0,1]上是增函数,在区间
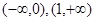上是减函数,又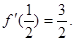
(Ⅰ)求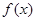
的解析式;
(Ⅱ)若在区间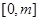
(m＞0)上恒有≤
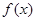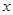成立,求m的取值范围.
袋中有大小、形状相同的红、黑球各一个，现一次有放回地随机摸取3次，每次摸取一个球
（Ⅰ）试问：一共有多少种不同的结果？请列出所有可能的结果；
（Ⅱ）若摸到红球时得2分，摸到黑球时得1分，求3次摸球所得总分为5的概率。
为了了解中学生的体能情况，抽取了某中学同年级部分学生进行跳绳测试，将所得的数据整理后画出频率分布直方图（如下图），已知图中从左到右的前三个小组的频率分别是0.1，0.3，0.4.第一小组的频数是5.
(1) 求第四小组的频率和参加这次测试的学生人数；
(2) 在这次测试中，学生跳绳次数的中位数落在第几小组内？
(3) 参加这次测试跳绳次数在100次以上为优秀，试估计该校此年级跳绳成绩的优秀率是多少？