(本小题满分12分)
曲线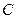 是以原点为中心,以抛物线
是以原点为中心,以抛物线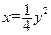 的焦点F为右焦点,离心率为
的焦点F为右焦点,离心率为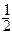 的椭圆,且过F的直线交椭圆C于P、Q两点,M是
的椭圆,且过F的直线交椭圆C于P、Q两点,M是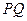 中点.
中点.
(1)求椭圆C的方程;
(2)当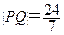 时,求直线PQ的方程.
时,求直线PQ的方程.
我们从小学开始,学过的数有:零、正整数、负整数、分数、整数、无理数、实数、有理数、虚数、纯虚数、非纯虚数、复数,画出数系的结构图.
.设p:实数x满足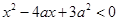 ,其中
,其中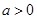 ,命题
,命题 实数
实数 满足
满足 .
.
(1)若 且
且 为真,求实数
为真,求实数 的取值范围;
的取值范围;
(2)若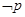 是
是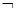
 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围.
的取值范围.
已知函数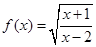 的定义域集合是A,函数
的定义域集合是A,函数 的定义域集合是B
的定义域集合是B
(1)求集合A、B
(2)若A B=B,求实数
B=B,求实数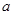 的取值范围.
的取值范围.
(12分)写出命题:“若 x+y =5,则 x = 3且 y = 2”的逆命题、否命题、逆否命题.并判断它们的真假.
如图,在棱长为1的正方体 中,
中,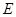 、
、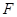 分别为
分别为 和
和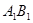 的中点.
的中点.
(1)求异面直线 和
和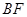 所成的角的余弦值;
所成的角的余弦值;
(2)求平面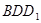 与平面
与平面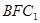 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;