．已知中心在原点O，焦点在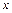
轴上，离心率为
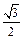的椭圆；以椭圆的顶点为顶点构成的四边形的面积为4．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若A\B分别是椭圆长轴的左．右端点，动点M满足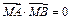
，直线MA交椭圆于P，求
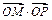的取值范围．
设函数
（Ⅰ）证明
其中为k为整数
（Ⅱ）设
为
的一个极值点，证明
（Ⅲ）设在（0,+∞）内的全部极值点按从小到大的顺序排列为
，证明：
在△ABC中，a、b、c分别为角A、B、C的对边，
表示该三角形的面积，且
（Ⅰ）求角
的大小；
（Ⅱ）若
，求b的值.
如图，函数y=2sin(π+φ),x∈R,(其中0≤φ≤
)的图象与y轴交于点（0，1）.
(Ⅰ)求φ的值；
(Ⅱ)设P是图象上的最高点，M、N是图象与x轴的交点，求
设函数f(x)=a·b，其中向量a=(2cosx，1)，b=(cosx， 
sin2x)，x∈R.
（Ⅰ）若f(x)=1-且x∈[-
，]，求x；
（Ⅱ）若函数y=2sin2x的图象按向量c=(m，n)(|m|<
)平移后得到函数y=f(x)的图象，求实数m、n的值。
为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校6名学生进行问卷调查，6人得分情况如下：5，6，7，8，9，10。把这6名学生的得分看成一个总体。（1）求该总体的平均数；（2）用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本。求该样本平均数与总体平均数之差的绝对值不超过0.5的概率。