如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1,ACC1A1均为正方形,∠BAC=90°,点D是棱B1C1中点.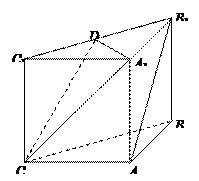
(1)求证:A1D⊥平面BB1C1C;
(2)求证:AB1∥平面A1DC;
(3)求二面角D-A1C-A的余弦值.
【2015高考重庆,文19】已知函数 (
( )在x=
)在x= 处取得极值.
处取得极值.
(Ⅰ)确定 的值,
的值,
(Ⅱ)若 ,讨论的单调性.
,讨论的单调性.
【2015高考浙江,文20】设函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的最小值
上的最小值 的表达式;
的表达式;
(2)已知函数 在
在 上存在零点,
上存在零点, ,求
,求 的取值范围.
的取值范围.
【2015高考新课标1,文21】(本小题满分12分)设函数 .
.
(Ⅰ)讨论 的导函数
的导函数 的零点的个数;
的零点的个数;
(Ⅱ)证明:当 时
时 .
.
【2015高考天津,文20】(本小题满分14分)已知函数
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)设曲线 与
与 轴正半轴的交点为P,曲线在点P处的切线方程为
轴正半轴的交点为P,曲线在点P处的切线方程为 ,求证:对于任意的正实数
,求证:对于任意的正实数 ,都有
,都有 ;
;
(Ⅲ)若方程 有两个正实数根
有两个正实数根 且
且 ,求证:
,求证: .
.
【2015高考四川,文21】已知函数f(x)=-2lnx+x2-2ax+a2,其中a>0.
(Ⅰ)设g(x)为f(x)的导函数,讨论g(x)的单调性;
(Ⅱ)证明:存在a∈(0,1),使得f(x)≥0恒成立,且f(x)=0在区间(1,+∞)内有唯一解.