.一个袋中装有四个形状大小完全相同的球,球的编号分别为 .
.
(Ⅰ)从袋中随机抽取两个球,求取出的球的编号之和不大于4的概率;
(Ⅱ)先从袋中随机取一个球,该球的编号为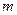 ,将球放回袋中,然后再从袋中随机取一个球,该球的编号为
,将球放回袋中,然后再从袋中随机取一个球,该球的编号为 ,求
,求 的概率.
的概率.
直线 与圆
与圆 交于
交于 、
、 两点,记△
两点,记△ 的面积为
的面积为 (其中
(其中 为坐标原点).
为坐标原点).
(1)当 ,
, 时,求
时,求 的最大值;
的最大值;
(2)当 ,
, 时,求实数
时,求实数 的值.
的值.
在正方体ABCD—A1B1C1D1中,E、F分别为棱BB1和DD1的中点. 
(1)求证:平面B1FC//平面ADE;
(2)试在棱DC上取一点M,使 平面ADE;
平面ADE;
(3)设正方体的棱长为1,求四面体A1—FEA的体积.
已知
(1)若 的单调递增区间;
的单调递增区间;
(2)若 的最大值为4,求a的值;
的最大值为4,求a的值;
(3)在(2)的条件下,求满足 集合。
集合。
某食品加工厂甲,乙两个车间包装小食品,在自动包装传送带上每隔30分钟抽取一袋食品,称其重量并将数据记录如下:
甲:102 100 98 97 103 101 99
乙: 102 101 99 98 103 98 99
(1)食品厂采用的是什么抽样方法(不必说明理由)?
(2)根据数据估计这两个车间所包装产品每袋的平均质量;
(3)分析哪个车间的技术水平更好些?
附:
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,f(x) 表示C到A距离4倍与C到B距离的6倍的和.
(1)求f(x)的解析式及其定义域;
(2)要使f(x)的值不超过70,x 应该在什么范围内取值?