如图, 是抛物线
是抛物线 的焦点,
的焦点, 为准线与
为准线与 轴的交点,直线
轴的交点,直线 经过点
经过点 .
.
(Ⅰ)直线 与抛物线有唯一公共点,求
与抛物线有唯一公共点,求 的方程;
的方程;
|
(Ⅱ)直线 与抛物线交于
与抛物线交于 、
、 两点记
两点记 、
、 的斜率分别为
的斜率分别为 ,
, .
.
 为定值;
为定值;
 在线段
在线段 上,且满足
上,且满足
 ,求点
,求点 的轨迹方程.
的轨迹方程.
函数 .
.
(Ⅰ)当 时,求
时,求 的最小值;
的最小值;
(Ⅱ)当 时,求
时,求 的单调区间.
的单调区间.
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB= ,
,
如图,O,H分别为AE、AB中点.
(Ⅰ)求证:直线OH//面BDE; (Ⅱ)求证:面ADE
(Ⅱ)求证:面ADE 面ABCE;
面ABCE;
(Ⅲ)求二面角O-DH-E的余弦值.
某次有奖竞猜活动设有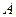 、
、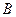 两组相互独立的问题,答对问题
两组相互独立的问题,答对问题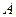 可赢得奖金3000元,答对问题
可赢得奖金3000元,答对问题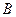 可赢得奖金6000元.规定答题顺序可任选,但只有一个问题答对后才能解答下一个问题,否则中止答题,假设你答对问题
可赢得奖金6000元.规定答题顺序可任选,但只有一个问题答对后才能解答下一个问题,否则中止答题,假设你答对问题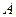 、
、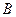 的概率依次为
的概率依次为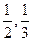 .
.
(Ⅰ)若你按先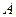 后
后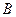 的次序答题,写出你获得奖金的数额
的次序答题,写出你获得奖金的数额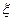 的分布列及期望
的分布列及期望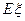 ;
;
(Ⅱ)你认为获得奖金期望的大小与答题顺序有关吗?证明你的结论.
已知函数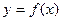 的图像关于直线
的图像关于直线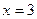 对称,当
对称,当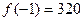 ,且
,且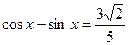 ,
,
求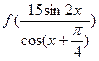 的值.
的值.