(本小题满分14分)如图,在四棱锥 中,底面
中,底面 是边长为
是边长为 的正方形,
的正方形, 、
、 分别为
分别为 、
、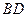 的中点,侧面
的中点,侧面 ,且
,且 .
.
(1)求证: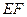 ∥平面
∥平面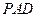 ;(2)求三棱锥
;(2)求三棱锥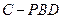 的体积.
的体积. 
(本大题共15分) 如图,F是椭圆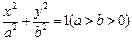 的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为
的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为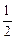 ,点C在x轴上,
,点C在x轴上,
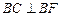 ,B、C、F三点确定的圆M恰好与
,B、C、F三点确定的圆M恰好与
直线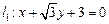 相切.(1)求椭圆的方程;
相切.(1)求椭圆的方程;
(2)过点A的直线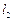 与圆M交于P、Q两点,
与圆M交于P、Q两点,
且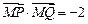 ,求直线
,求直线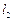 的方程.
的方程.
(本大题共14分)一袋中装有分别标记着1,2,3,4数字的4只小球,每次从袋中取出一只球,设每只小球被取到的可能性相同.(1)若每次取出的球不放回袋中,求恰好第三次取到标号为3的球的概率;(2)若每次取出的球放回袋中,然后再取出一只球,现连续取三次球,若三次取出的球中标号最大的数字为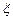 ,求
,求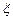 的概率分布列与期望.
的概率分布列与期望.
(本大题共14分)已知数列 的前n项和
的前n项和 ,且
,且 是
是 与1的等差中项.
与1的等差中项.
(1)求数列 和数列
和数列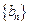 的通项公式;(2)若
的通项公式;(2)若 ,求
,求 ;
;
(3)若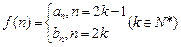 ,是否存在
,是否存在 使得
使得 ,并说明理由.
,并说明理由.
(本大题共14分)已知函数 (
( 为常数),若函数
为常数),若函数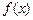 的最大值为
的最大值为 .(1)求实数
.(1)求实数 的值;(2)将函数
的值;(2)将函数 的图象向左平移
的图象向左平移 个单位,再向下平移2个单位得到函数
个单位,再向下平移2个单位得到函数 的图象,求函数
的图象,求函数 的单调递减区间.
的单调递减区间.
已知函数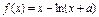 在
在 处取得极值。
处取得极值。
(1)求实数 的值;(2)若关于
的值;(2)若关于 的方程
的方程 在
在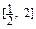 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数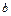 的取值范围;(3)证明:
的取值范围;(3)证明: 。参考数据:
。参考数据: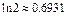 。
。