如图,ABCD是边长为2的正方形,O是正方形的中心,PO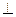 底面ABCD,PO=
底面ABCD,PO=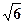 ,E是PC的中点。
,E是PC的中点。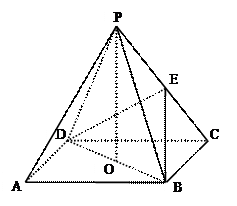
求证:(1)PA∥平面BDE;(2)直线PA与平面PBD所成的角.
已知复数 ,
, ,且
,且 .
.
(1)若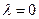 且
且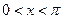 ,求
,求 的值;
的值;
(2)设 =
=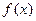 ,求
,求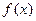 的最小正周期和单调减区间.
的最小正周期和单调减区间.
已知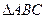 中,
中, ,
, ,
, ,记
,记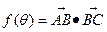 ,
,
(1)求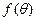 关于
关于 的表达式;
的表达式;
(2)求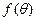 的值域;
的值域;
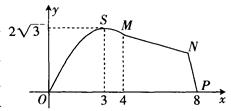
如图,我市拟在长为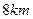 的道路
的道路 的一侧修建一条运动赛道。赛道的前一部分为曲线段
的一侧修建一条运动赛道。赛道的前一部分为曲线段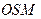 ,该曲线段为函数
,该曲线段为函数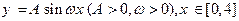 的图像,且图像的最高点为
的图像,且图像的最高点为 ;赛道的后一部分为折线段
;赛道的后一部分为折线段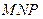 ,为保证参赛运动员的安全,限定
,为保证参赛运动员的安全,限定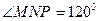 。
。
(1)求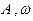 的值和
的值和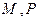 两点间的距离
两点间的距离
(2)应如何设计,才能使折线段赛道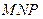 最长
最长
在 中,
中, 为锐角,角
为锐角,角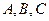 所对应的边分别为
所对应的边分别为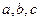 ,且
,且
(I)求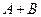 的值;
的值;
 (II)若
(II)若 ,求
,求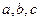 的值。
的值。
已知函数
(Ⅰ)求
的单调区间;
(Ⅱ)记
在区间
(
)上的最小值为
令
.
(ⅰ)如果对一切
,不等式
恒成立,求实数
的取值范围;
(ⅱ)求证:
.