(本小题满分12分)
已知函数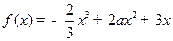 .
.
(Ⅰ)当 时,求函数
时,求函数 在
在 ,
,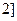 上的最大值、最小值;
上的最大值、最小值;
(Ⅱ)令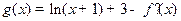 ,若
,若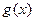 在
在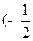 ,
, 上单调递增,求实数
上单调递增,求实数 的取值范围.
的取值范围.
(本小题满分13分)设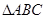 的内角
的内角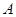 ,
,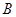 ,
,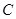 所对边的长分别是
所对边的长分别是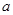 ,
,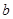 ,
,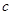 ,且
,且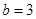 ,
,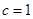 ,
,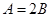 .
.
(1)求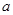 的值;
的值;
(2)求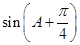 的值.
的值.
(本小题满分13分)某校书法兴趣组有 名男同学
名男同学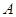 ,
,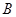 ,
,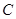 和
和 名女同学
名女同学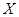 ,
,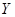 ,
,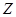 ,其年级情况如下表:
,其年级情况如下表:
| 一年级 |
二年级 |
三年级 |
|
| 男同学 |
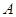 |
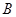 |
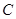 |
| 女同学 |
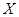 |
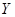 |
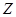 |
现从这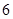 名同学中随机选出
名同学中随机选出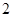 人参加书法比赛(每人被选到的可能性相同).
人参加书法比赛(每人被选到的可能性相同).
(1)用表中字母列举出所有可能的结果;
(2)设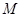 为事件“选出的
为事件“选出的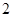 人来自不同年级且性别相同”,求事件
人来自不同年级且性别相同”,求事件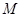 发生的概率.
发生的概率.
(本小题满分14分)已知函数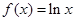 ,
,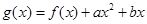 ,函数
,函数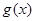 的图象在点
的图象在点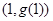 处的切线平
处的切线平
行于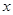 轴.
轴.
(1)确定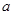 与
与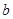 的关系;
的关系;
(2)试讨论函数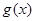 的单调性;
的单调性;
(3)证明:对任意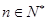 ,都有
,都有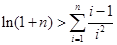 成立.
成立.
(本小题满分14分)已知等差数列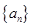 的公差为
的公差为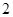 ,前
,前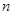 项和为
项和为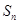 ,且
,且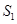 ,
,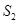 ,
,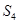 成等比数列.
成等比数列.
(1)求数列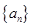 的通项公式;
的通项公式;
(2)令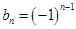
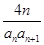 ,求数列
,求数列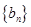 的前
的前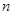 项和
项和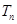 .
.
(本小题满分13分)已知椭圆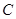 :
: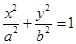
 的焦距为
的焦距为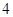 ,其短轴的两个端点与长轴的一个端点构成正三角形.
,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆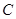 的标准方程;
的标准方程;
(2)设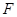 为椭圆
为椭圆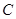 的左焦点,
的左焦点,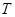 为直线
为直线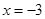 上任意一点,过
上任意一点,过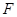 作
作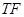 的垂线交椭圆
的垂线交椭圆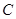 于点
于点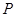 ,
,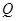 ,
,
①证明: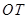 平分线段
平分线段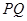 (其中
(其中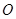 为坐标原点),
为坐标原点),
②当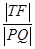 值最小时,求点
值最小时,求点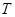 的坐标.
的坐标.