(本小题满分12分)
某企业生产的一批产品中有一、二、三等品及次品共四个等级,1件不同等级产品的利润
(单位:元)如表1,从这批产品中随机抽取出1件产品,该件产品为不同等级的概率如表2.
若从这批产品中随机抽取出的1件产品的平均利润(即数学期望)为 元.
元.
| 等级 |
一等品 |
二等品 |
三等品 |
次品 |
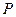 |
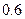 |
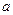 |
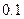 |
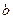 |
| 等级 |
一等品 |
二等品 |
三等品 |
次品 |
| 利润 |
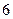 |
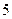 |
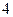 |
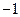 |
表1 表2
(1) 求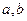 的值;
的值;
(2) 从这批产品中随机取出3件产品,求这3件产品的总利润不低于17元的概率.
在三棱柱 中,已知
中,已知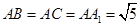 ,
, ,
,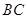 的中点为
的中点为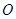 ,
,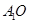 垂直于底面
垂直于底面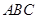 .
.
(1)证明:在侧棱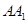 上存在一点
上存在一点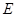 ,使得
,使得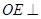 平面
平面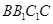 ,并求出
,并求出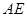 的长;
的长;
(2)求二面角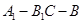 的平面角的余弦值.
的平面角的余弦值.
已知椭圆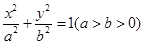 的右焦点为
的右焦点为 ,
,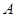 为短轴的一个端点,且
为短轴的一个端点,且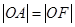 ,
, 的面积为1(其中
的面积为1(其中 为坐标原点).
为坐标原点).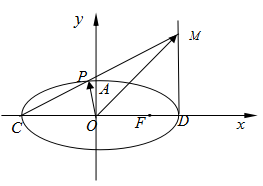
(1)求椭圆的方程;
(2)若 ,
,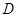 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点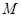 满足
满足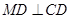 ,连接
,连接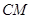 ,交椭圆于点
,交椭圆于点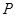 ,证明:
,证明: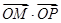 为定值.
为定值.
某班共有36名学生,其中有班干部6名,现从36名同学中任选2名代表参加某次活动,求:
(1)恰有1名班干部当选代表的概率;
(2)至少有1名班干部当选代表的概率;
(3)已知36名学生中男生比女生多,若选得同性代表的概率等于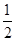 ,则男生比女生多几人?
,则男生比女生多几人?
已知函数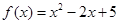 ,
, .
.
(1)是否存在实数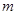 ,使不等式
,使不等式 对于
对于 恒成立,并说明理由;
恒成立,并说明理由;
(2)若至少存在一个实数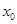 ,使不等式
,使不等式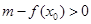 成立,求实数
成立,求实数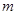 的取值范围.
的取值范围.
如图,在三棱柱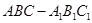 中,侧棱垂直于底面,
中,侧棱垂直于底面,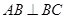 ,
,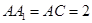 ,
,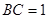 ,
, ,
,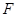 分别是
分别是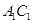 ,
,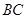 的中点.
的中点.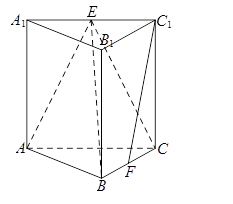
(1)求证:平面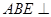 平面
平面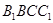 ;
;
(2)求证: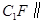 平面
平面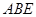 ;
;
(3)求三棱锥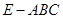 的体积.
的体积.