（本小题满分14分）
建造一容积为8
深为2m的长方体形无盖水池，每
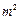池底和池壁造价各为120元和80元.
（1）求总造价关于一边长x的函数解析式，并指出该函数的定义域；
（2）判断（1）中函数在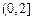
和
上的单调性；
（3）如何设计水池尺寸，才能使总造价最低；
已知函数f（x）=log2(x2-ax-a)在区间（-∞,1-
］上是单调递减函数.求实数a的取值范围.
设函数f(x)是定义在R上的增函数，且f(x)≠0，对于任意x1、x2∈R，都有f(x1+x2)=f(x1)·f(x2).
(1)求证：f(x1-x2)=
；
(2)若f(1)=2，解不等式f(3x)>4f(x).
已知f(x)=
+a为奇函数.
(1)求a的值；
(2)求函数的单调区间.
若函数y=
为奇函数，
(1)确定a的值；
(2)求函数的定义域；
(3)求函数的值域；
(4)讨论函数的单调性.
求下列函数的定义域与值域：
(1)y=
；
(2)y=(
)|x|；
(3)y=4x+2x+1+1；
(4)y=
.