(本小题满分12分)已知函数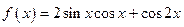 (
(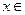 R).
R).
(1)求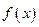 的最小正周期和最大值;
的最小正周期和最大值;
(2)若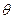 为锐角,且
为锐角,且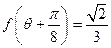 ,求
,求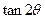 的值.
的值.
(本小题满分12分)如图,在四棱锥 中,
中,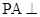 平面
平面 ,
,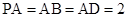 ,四边形
,四边形 满足
满足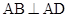 ,
, 且
且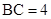 ,点
,点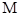 为
为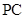 中点,点
中点,点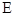 为
为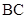 边上的动点,且
边上的动点,且 .
.
(1)求证:平面 平面
平面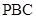 ;
;
(2)是否存在实数 ,使得二面角
,使得二面角 的余弦值为
的余弦值为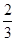 ?若存在,试求出实数
?若存在,试求出实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本题12分)已知数列 的前
的前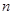 项和为
项和为 ,且
,且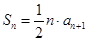 ,其中
,其中
(1)求数列 的通项公式;
的通项公式;
(2)若 ,数列
,数列 的前
的前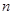 项和为
项和为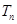 ,求证:
,求证:
【改编】(本小题满分12分)函数 部分图象如图所示.
部分图象如图所示.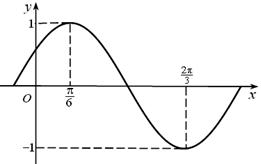
(Ⅰ)求 的最小正周期及解析式;
的最小正周期及解析式;
(Ⅱ)设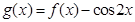 ,求函数
,求函数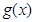 在区间
在区间 上的单调性.
上的单调性.
设函数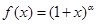 的定义域是
的定义域是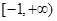 ,其中常数
,其中常数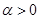 .
.
(1)若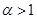 ,求
,求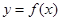 的过原点的切线方程.
的过原点的切线方程.
(2)当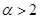 时,求最大实数
时,求最大实数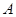 ,使不等式
,使不等式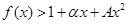 对
对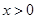 恒成立.
恒成立.
(3)证明当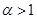 时,对任何
时,对任何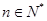 ,有
,有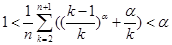 .
.
(本小题满分13分)已知椭圆C: (a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程.
(2)设F为椭圆C的左焦点,T为直线x=-3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当 最小时,求点T的坐标.
最小时,求点T的坐标.